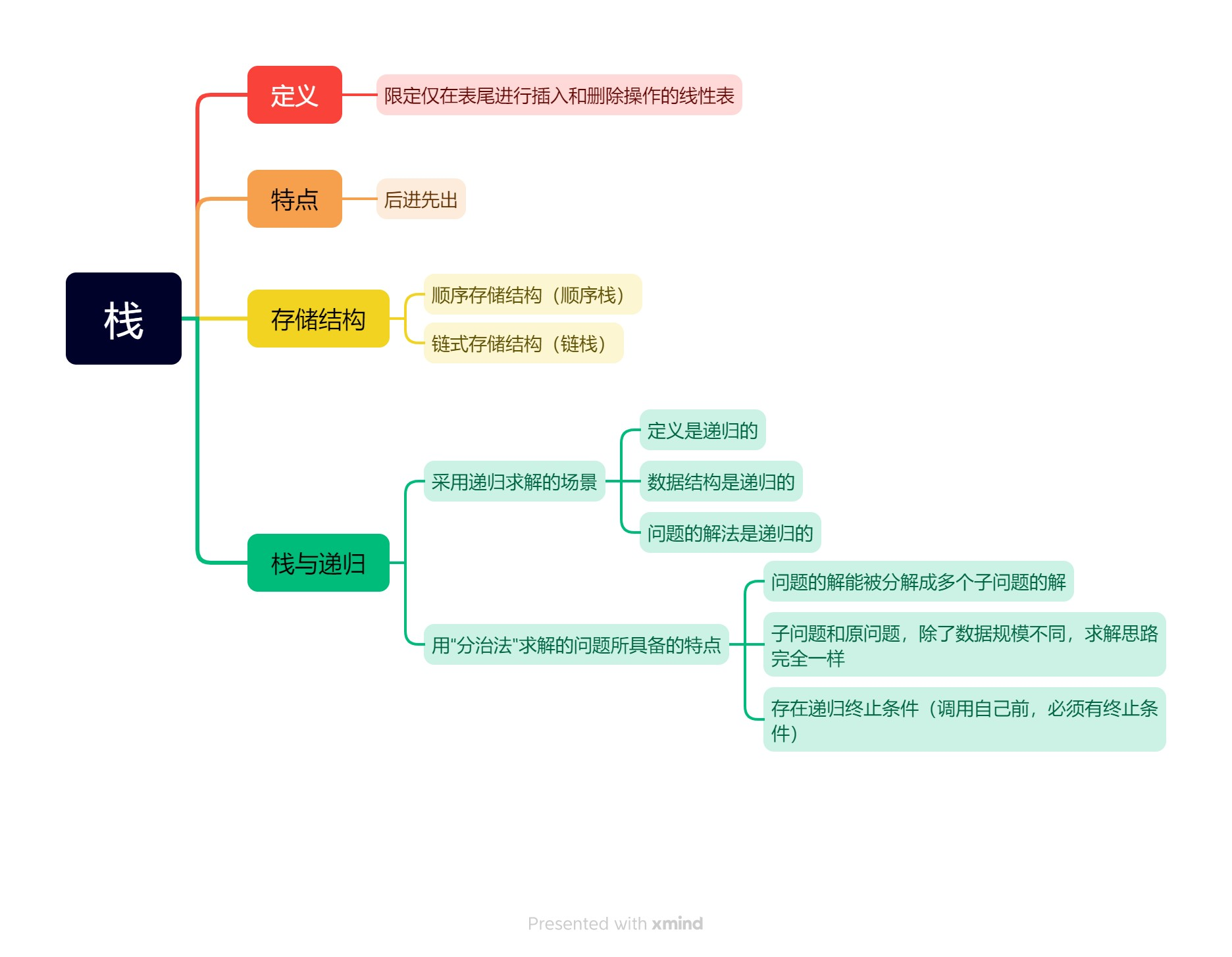
数据结构：栈

线性结构，除了最基础的线性表外，还有一类特殊的线性表。本篇文章要讨论的栈就是一个特殊的线性表，它在计算机系统中有着举足轻重的作用，比如，在函数调用的实现过程中就用到了栈这个数据结构。栈是一个非常基础的数据结构，因此也需重点掌握。

一、简介

栈（Stack）是限定仅在表尾进行插入和删除操作的线性表。对于栈来说，插入、删除的一端（即表尾）称为栈顶（top），另一端则称为栈底（bottom）。

栈的操作是按后进先出的原则进行的。因此，栈又被称为后进先出（Last in First Out, LIFO）的线性表。假设栈S=($a_1$, $a_2$, …, $a_n$)，若栈中元素是按$a_1$, $a_2$, …, $a_n$的顺序依次进栈的，则称$a_1$为栈底元素，$a_n$为栈顶元素，其退栈次序是$a_n$, …, $a_2$, $a_1$。栈的这个特点可用铁路调度站形象地表示。

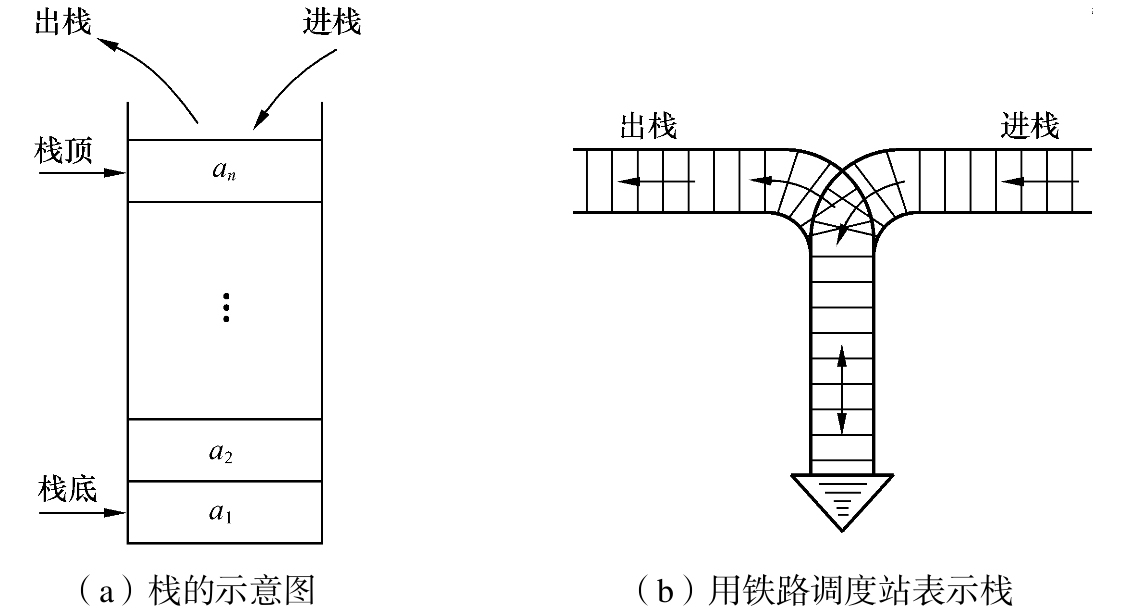
在日常生活中，有很多类似栈的例子。例如，洗盘子时，总是将已经洗好的盘子逐个往上叠放，而用盘子时则是从上往下逐个取用。栈就是对上述场景的抽象。在程序设计中，如果需要按照与保存数据时相反的顺序来使用数据，则可以利用栈来实现。

和线性表类似，栈也有两种存储结构，分别是顺序栈和链栈。

二、顺序栈

顺序栈，是指采用顺序存储结构实现的栈。

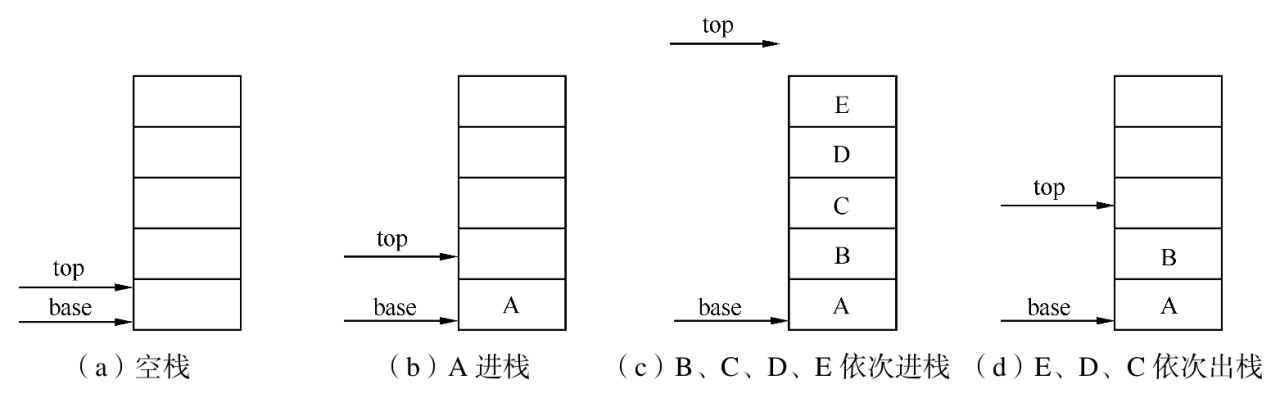
顺序栈也是用数组实现的。由于栈顶位置会随着进栈和出栈操作而变化，所以需要用一个指针top指示栈顶元素在顺序栈中的位置，这里的top通常被称为栈顶指针。又因为栈底位置是固定不变的，故可以将栈底位置设置在数组的最低端。

鉴于C语言中，数组下标约定从0开始，当以C语言作为描述语言时，上述设定会带来很大不便，因此另设指针base指示栈底元素在顺序栈中的位置。当top和base的值相等时，表示空栈。

在C语言中，顺序栈的类型描述如下：

// 栈空间的大小应根据实际需要来定义，这里假设为100
#define MAXSIZE 100

// SElemType的类型可根据实际情况而定，这里假设为char
typedef char SElemType;

typedef struct {
    // 栈顶指针
    SElemType *top;
    // 栈底指针
    SElemType *base;
    // 栈可用的最大容量
    int stacksize;
}SqStack;

说明：

• base为栈底指针，初始化完成后，栈底指针base始终指向栈底的位置。若base的值为NULL，则表明栈结构不存在。
• top为栈顶指针，其初值指向栈底。每当插入新的栈顶元素时，指针top增1；删除栈顶元素时，指针top减1。因此，栈空时，top和base的值相等，都指向栈底；栈非空时，top始终指向栈顶元素的上一个位置。
• stacksize指示栈可使用的最大容量，初始化操作会为顺序栈分配MAXSIZE大小的数组空间，将stacksize置为MAXSIZE。

2.1、初始化

初始化，就是为顺序栈动态分配一个预定义大小的数组空间。该算法的步骤为：

• 为顺序栈动态分配一个最大容量为MAXSIZE的数组空间，使base指向这段空间的基地址，即栈底。
• 栈顶指针top初始为base，表示栈为空。
• stacksize置为栈的最大容量MAXSIZE。

相应的算法描述为：

// 构造一个空栈S
Status InitStack(SqStack &S) {
    // 为顺序栈分配一个最大容量为MAXSIZE的数组空间
    S.base=(SElemType *)malloc(sizeof(SElemtype) * MAXSIZE);
    // 存储分配失败
    if(!S.base) exit(OVERFLOW);
    // top初始为base
    S.top=S.base;
    // stacksize置为栈的最大容量MAXSIZE
    S.stacksize=MAXSIZE;
    
    return OK;
}

2.2、入栈

入栈，是指在栈顶插入一个新的元素。该算法的步骤为：

• 判断栈是否满，若满则返回ERROR。
• 将新元素压入栈顶，栈顶指针加1。

相应的算法描述为：

Status Push(SqStack &S, SElemType e) {
    // 栈满
    if(S.top-S.base==S.stacksize) return ERROR;
    // 元素e压入栈顶，栈顶指针加1
    *S.top++=e;
    
    return OK;
}

2.3、出栈

出栈，是将栈顶元素删除。该算法的步骤为：

• 判断栈是否空，若空则返回ERROR。
• 栈顶指针减1，栈顶元素出栈。

相应的算法描述为：

Status Pop(SqStack &S, SElemType &e) {
    // 栈空
    if(S.top==S.base) return ERROR;
    // 栈顶指针减1，将栈顶元素赋给e
    e=*--S.top;
    
    return OK;
}

2.4、取栈顶元素

当栈非空时，返回当前栈顶元素的值，栈顶指针保持不变。相应的算法描述为：

SElemType GetTop(SqStack s) {
    if(S.top!=S.base)
        return *(S.top-1);
}

2.5、溢出问题

在顺序栈中，常常会发生溢出问题。当栈满时，再做进栈操作，就会溢出，简称“上溢”；当栈空时，再做出栈操作，也会溢出，简称“下溢”。

在实际应用中，可能同时使用多个栈。为了防止溢出，需要为每个栈分配一个较大的空间，而这往往会产生空间上的浪费。因为当某一个栈发生溢出的同时，其余的栈还可能有很多的未用空间。如果将多个栈分配在同一个顺序存储空间内，即让多个栈共享存储空间，就可以相互进行调节，既节约了空间，又可降低发生溢出的频率。

当程序中同时使用两个栈时，可以将两个栈的栈底分别设在顺序存储空间的两端，让两个栈顶各自向中间延伸。当一个栈中的元素较多而栈使用的空间超过共享空间的一半时，只要另一个栈中的元素不多，就可以让第一个栈占用第二个栈的部分存储空间。只有当整个存储空间被两个栈占满时（即两栈顶相遇），才会产生溢出。

为了克服顺序栈存在溢出和空间浪费问题，还可以采用链式存储结构来存储栈。

三、链栈

链栈，是指采用链式存储结构实现的栈。

由于栈的主要操作是在栈顶插入和删除，显然以链表的头部作为栈顶是最方便的，而且没必要像单链表那样为了操作方便附加一个头结点。

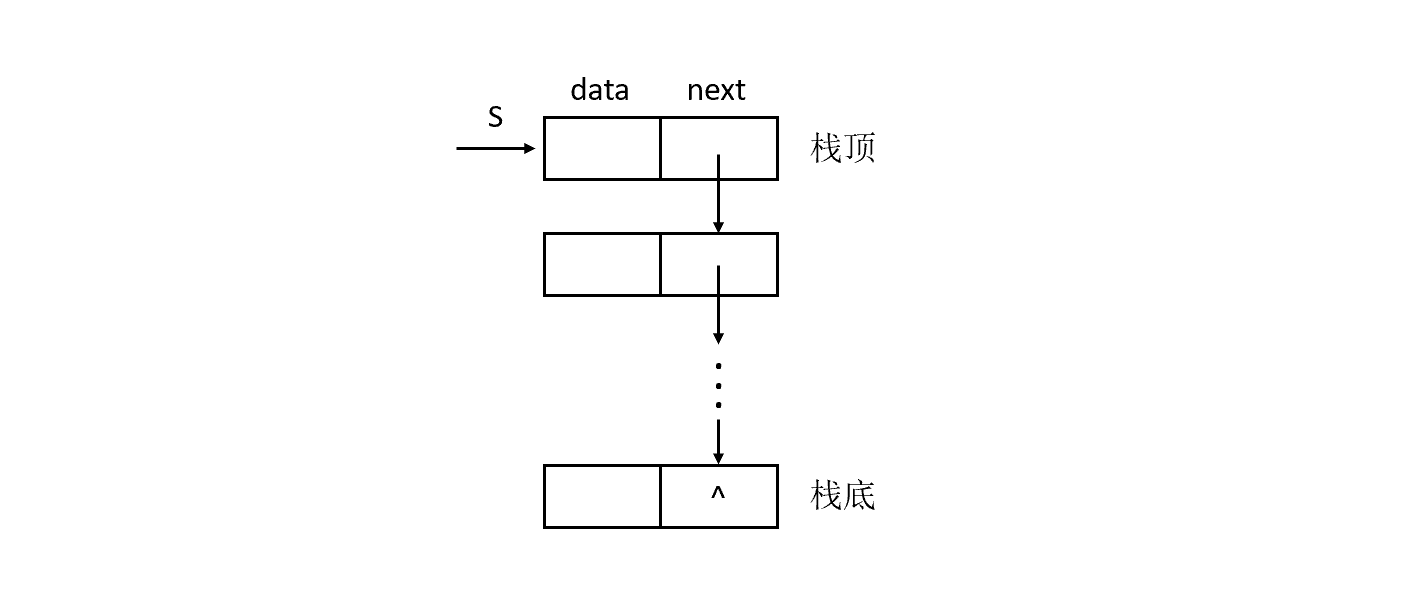
在C语言中，链栈的类型描述如下：

typedef struct StackNode {
    SElemType data;
    struct StackNode *next;
}StackNode, *LinkStack;

3.1、初始化

链栈的初始化操作就是构造一个空栈，因为不用设头结点，所以直接将栈顶指针置空即可。相应的算法描述为：

// 构造一个空栈S，栈顶指针置空
Status InitStack(LinkStack &S) {
    S=NULL;
    
    return OK;
}

3.2、入栈

和顺序栈的入栈操作不同，链栈在入栈前不需要判断栈是否满，只需要为入栈元素动态分配一个结点空间。

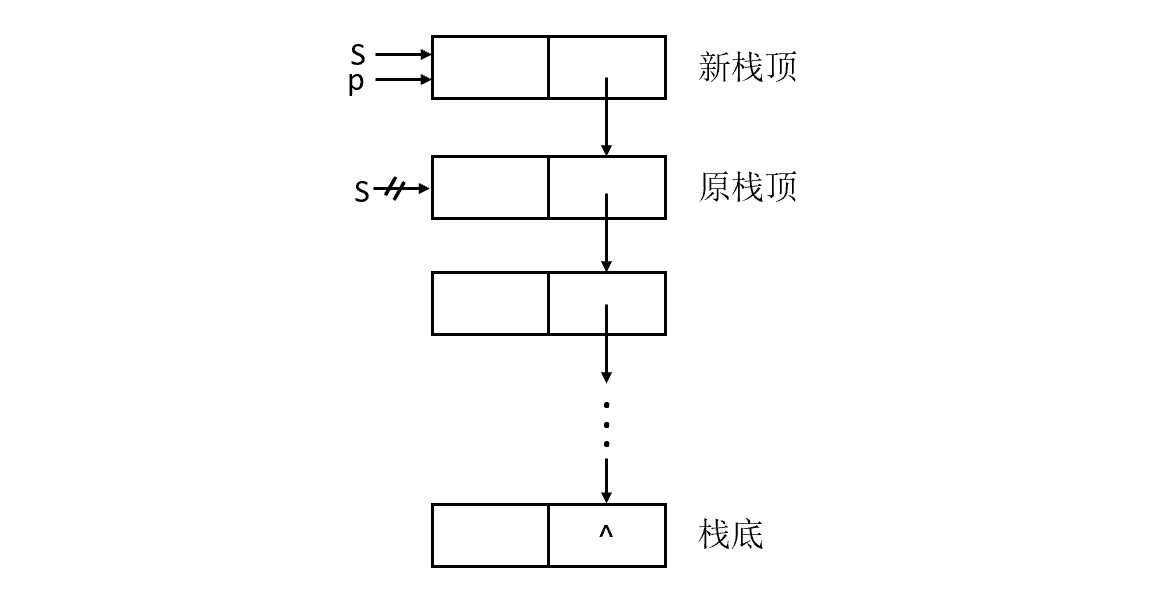
该算法步骤为：

• 为入栈元素e分配空间，用指针p指向。
• 将新结点数据域置为e。
• 将新结点插入栈顶。
• 修改栈顶指针为p。

相应的算法描述为：

Status Push(LinkStack &S, SElemType e) {
    p=(SElemType *)malloc(sizeof(SElemtype));
    p->data=e;
    p->next=S;
    S=p;
    
    return OK;
}

3.3、出栈

和顺序栈一样，链栈在出栈前也需要判断栈是否为空，不同的是，链栈在出栈后需要释放出栈元素的栈顶空间。

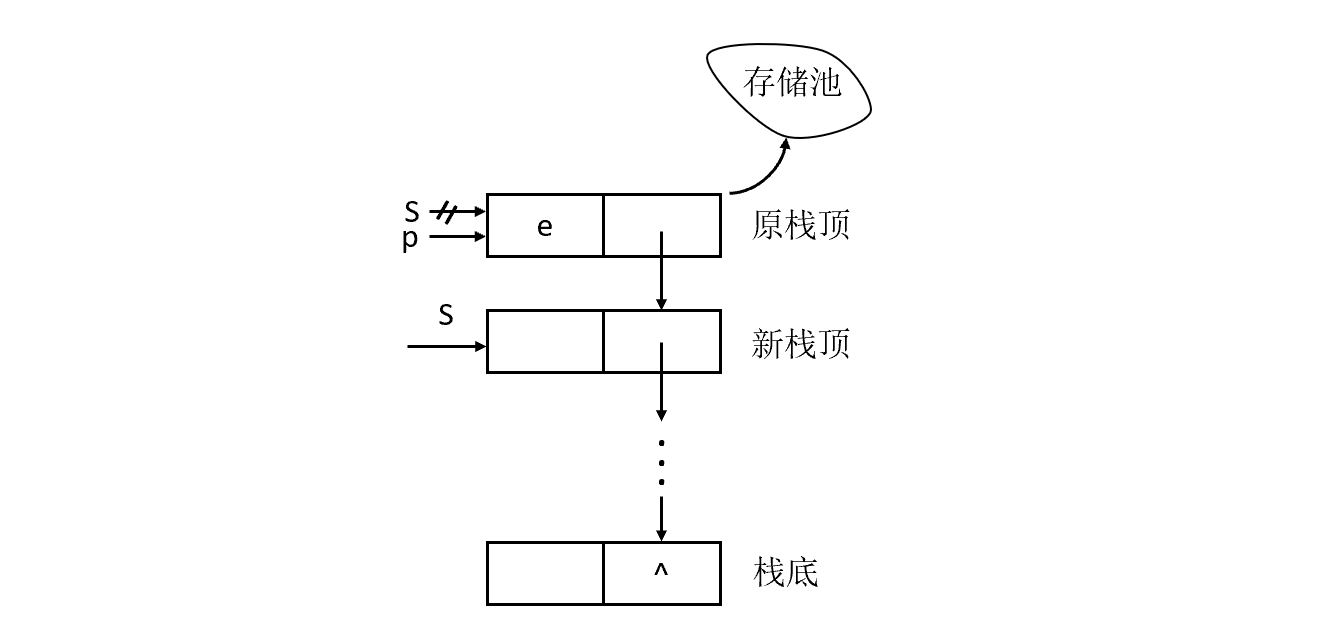
该算法步骤为：

• 判断栈是否为空，若空则返回ERROR。
• 将栈顶元素赋给e。
• 临时保存栈顶元素的空间，以备释放。
• 修改栈顶指针，指向新的栈顶元素。
• 释放原栈顶元素的空间。

相应的算法描述为：

Status Pop(LinkStack &S, SElemType &e) {
    if(S==NULL) return ERROR;
    
    e=S->data;
    p=S;
    S=S->next;
    free(p);
    
    return OK;
}

3.4、取栈顶元素

与顺序栈一样，当栈非空时，返回当前栈顶元素的值，栈顶指针S保持不变。相应的算法描述为：

SElemType GetTop(LinkStack S) {
    if(S!=NULL) return S->data;
}

四、栈与递归

栈的一个重要应用是，在程序设计语言中，实现递归。所谓递归，是指在一个函数、过程或者数据结构定义的内部又直接（或间接）地出现本身。递归函数，就是一个直接（或间接）调用自己的函数。

4.1、采用递归算法求解的场景

在以下3种情况中，常常会使用递归的方法。

• 定义是递归的
• 数据结构是递归的
• 问题的解法是递归的

4.1.1、定义是递归的

在数学中，有很多函数是递归定义的。比如，阶乘函数，其定义如下：

Fact(n)=n*Fact(n-1)，其中f(0)=1

该函数就可用递归来求解，相应的算法描述为：

long Fact(long n) {
    // 递归终止条件
    if(n==0) return 1;
    // 递归步骤
    else return n*Fact(n-1);
}

如下图，是主程序调用函数Fact (4)的执行过程：

在执行过程中，依次以参数4、3、2、1、0执行递归调用。最后一次递归调用时，因参数n为0执行if语句，递归终止，逐步返回，返回时依次计算1*1、2*1、3*2、4*6，最后将计算结果24返回给主程序。

4.1.2、数据结构是递归的

有些数据结构其本身具有递归的特性。

比如，在单链表中，结点LNode的定义由数据域data和指针域next组成，其中指针域next是一种指向LNode类型的指针，也即LNode的定义中又用到了其自身，所以，链表是一种递归的数据结构。

对于递归的数据结构，相应算法可采用递归的方法来实现。如下，是从前向后遍历输出链表结点的递归算法：

void TraverseList(LinkList p) {
    // 递归终止条件
    if(p==NULL) return;
    else {
        // 输出当前结点的数据域
        con<<p->data<<endl;
        // 递归输出后继结点
        TraverseList(p->next);
    }
}

调用此递归函数时，参数p指向单链表的首元结点，在递归过程中，p不断指向后继结点，直到p为NULL时递归结束。

4.1.3、问题的解法是递归的

还有一类问题，虽然问题本身没有明显的递归结构，但用递归求解比用迭代求解更简单。

比如，Hanoi塔问题。如下图，假设有3个分别命名为A、B和C的塔座，在塔座A上插有n个直径大小各不相同，依小到大编号为1，2，…，n的圆盘。

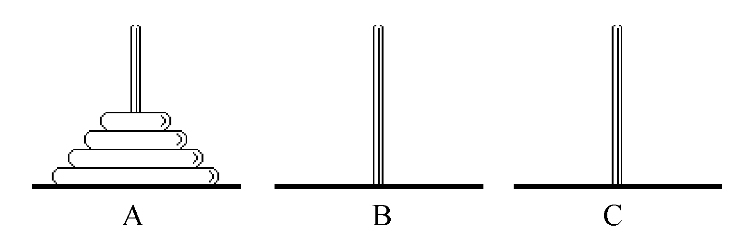
现要求将塔座A上的n个圆盘移至塔座C上，并仍按同样顺序叠排，圆盘移动时必须遵循下列规则：

• 每次只能移动一个圆盘；

• 圆盘可以插在A、B和C中的任一塔座上；

• 任何时刻都不能将一个较大的圆盘压在较小的圆盘之上。

如何实现移动圆盘的操作呢？可以用递归方法来解决这个问题。设A柱上最初的盘子总数为n，则当n=1时，只要将编号为1的圆盘直接从塔座A移至塔座C上即可；否则，执行以下三步：

• 用C柱做过渡，将A柱上的(n-1)个盘子移到B柱上；

• 将A柱上最后一个盘子直接移到C柱上；

• 用A柱做过渡，将B柱上的（n-1）个盘子移到C柱上。

在这个解法中，如何将n−1个圆盘从一个塔座移至另一个塔座的问题是一个和原问题具有相同特征属性的问题，只是问题的规模小1，因此可以用同样的方法求解。该解法的移动过程如下所示（图中n=4）：

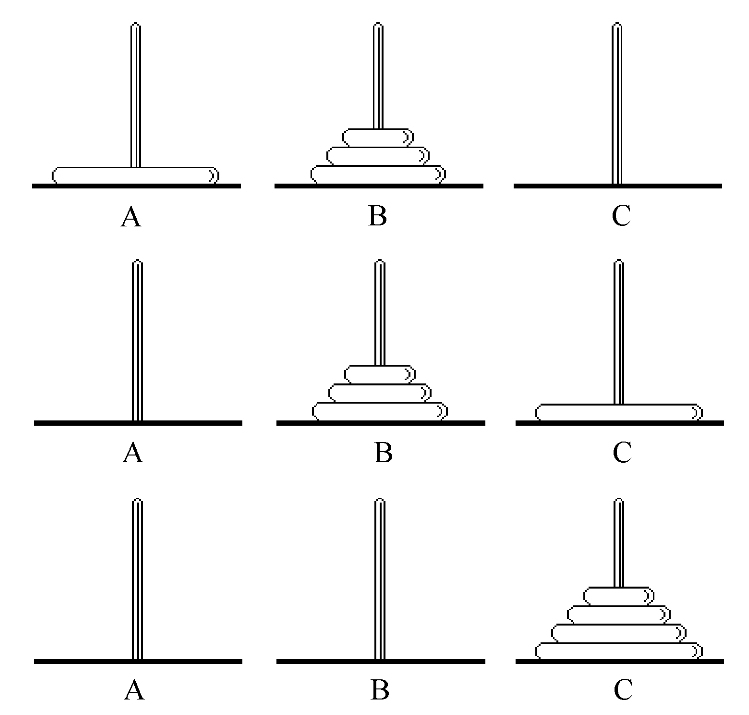
上述解法的算法步骤为：

• 如果n=1，则直接将编号为1的圆盘从A移到C，递归结束。
• 否则：
  • 递归，将A上编号为1至n-1的圆盘移到B，C做辅助塔；
  • 直接将编号为n的圆盘从A移到C；
  • 递归，将B上编号为1至n-1的圆盘移到C，A做辅助塔。

相应的算法描述为：

// 为了便于描述算法，将搬动操作定义为move(A,n,C)，即将编号为n的圆盘从A移到C，同时设一个初值为0的全局变量m，对搬动进行计数。
int m=0;

void move(char A, int n, char C) {
    count<<++m<<","<<n<<","<<A<<","<<C<<endl;
}

// 将塔座A上的n个圆盘按规则搬到C上，B做辅助塔
void Hanoi(int n, char A, char B, char C) {
    // 将编号为1的圆盘从A移到C
    if(n==1) move(A, 1, C);
    else {
        // 将A上编号为1至n-1的圆盘移到B，C做辅助塔
        Hanoi(n-1, A, C, B);
        // 将编号为n的圆盘从A移到C
        move(A, n, C);
        // 将B上编号为1至n-1的圆盘移到C，A做辅助塔
        Hanoi(n-1, B, A, C);
    }
}

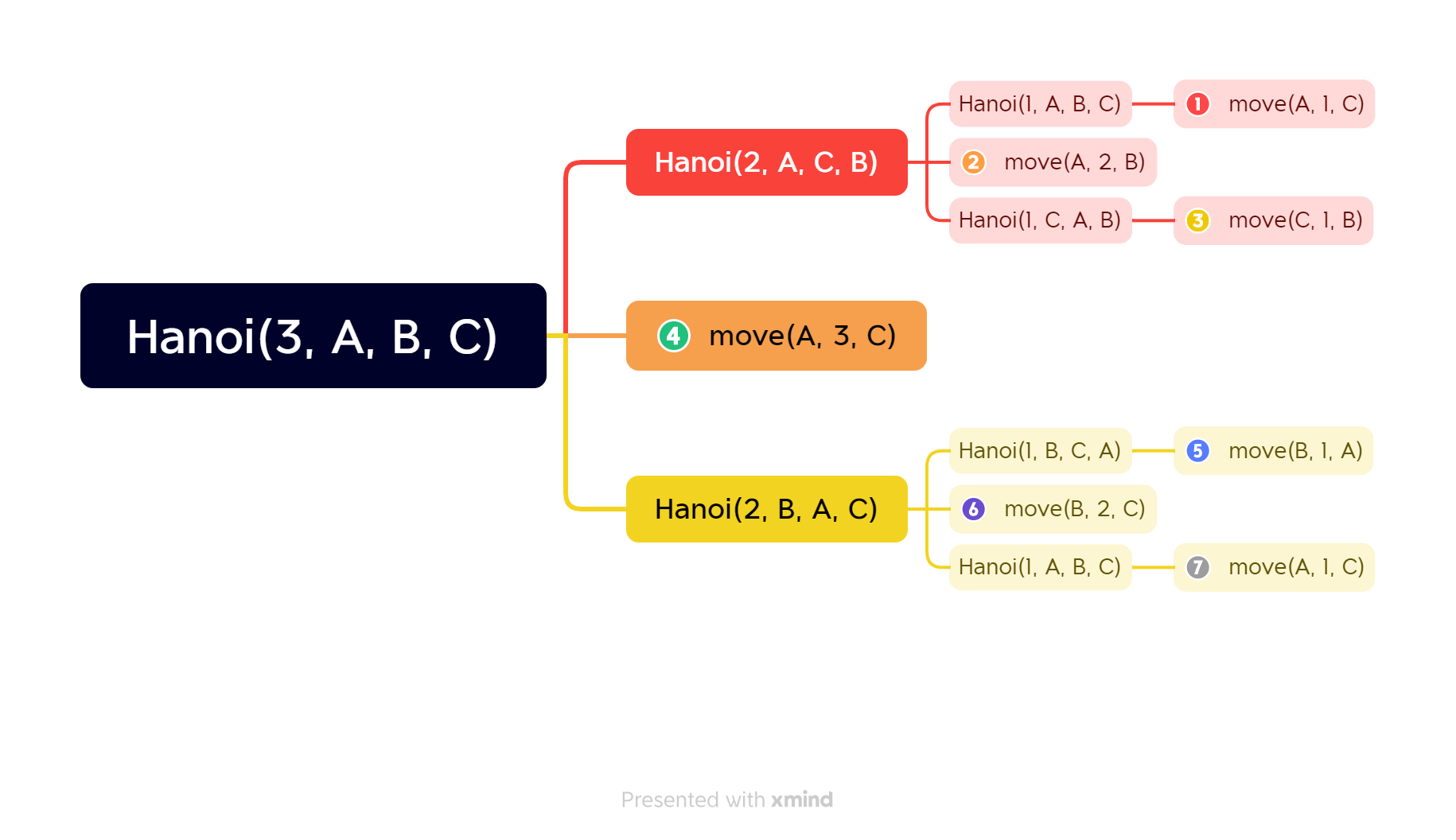
如下图，是Hanoi(3)的执行过程：

4.1.4、小结

上述问题其实都采用了一种分解-求解的策略，即将一个复杂问题，分解成几个相对简单且解法相同或类似的子问题来求解。比如，在阶乘函数中，计算4!时，先计算3!。

分解-求解的策略又被称为“分治法”。通常，一个问题若能采用“分治法”进行递归求解，就必须同时满足以下三个条件：

• 这个问题的解，能被分解成多个子问题的解。
• 子问题和原问题，除了数据规模不同，求解思路完全一样。
• 存在递归终止条件（调用自己前，必须有终止条件）。

相应算法的一般形式可以描述为：

void p(参数表) {
    if(递归终止条件成立) 直接求解；
    else p(较小的参数);
}

4.2、递归过程与递归工作栈

递归函数在执行过程中，需进行多次自我调用。那么，这个递归函数是如何执行的呢？

4.2.1、嵌套调用

在回答上述问题之前，我们先看任意两个函数之间进行调用的情形。通常，当一个函数在运行期间调用另一个函数时，在运行被调用函数之前，系统需先完成3件事：

• 保存调用函数的所有参数、返回地址等信息；

• 为被调用函数的局部变量分配存储区；

• 将控制转移到被调用函数的入口。

而从被调用函数返回调用函数之前，系统也应完成3件工作：

• 保存被调用函数的计算结果；
• 释放被调用函数的数据区；
• 依照被调用函数保存的返回地址将控制转移到调用函数。

当有多个函数构成嵌套调用时，按照“后调用先返回”的原则，上述函数之间的信息传递和控制转移必须通过“栈”来实现，即系统将整个程序运行时所需的数据空间安排在一个栈中，每当调用一个函数时，就为它在栈顶分配一个存储区，每当从一个函数退出时，就释放它的存储区，则当前正运行的函数的数据区必在栈顶。

下面，我们通过具体示例来理解上述内容，假设有如下代码：

void first(int s, int t);

void second(int d);

void main() {
    int m,n;
    ...
    first(m,n);
    RetLoc1: ...
}

int first(int s, int t) {
    int i;
    ...
    second(i);
    RetLoc2: ...
}

int second(int d) {
    int x, y;
    ...
}

在这段代码中，主函数main中调用了函数first（调用完之后的返回地址是RetLoc1），而在函数first中又调用了函数second（调用完之后的返回地址是RetLoc1）。如下图，左图是执行函数second中某个语句时栈的状态，右图是从函数second退出之后，执行函数first中某个语句时的状态：

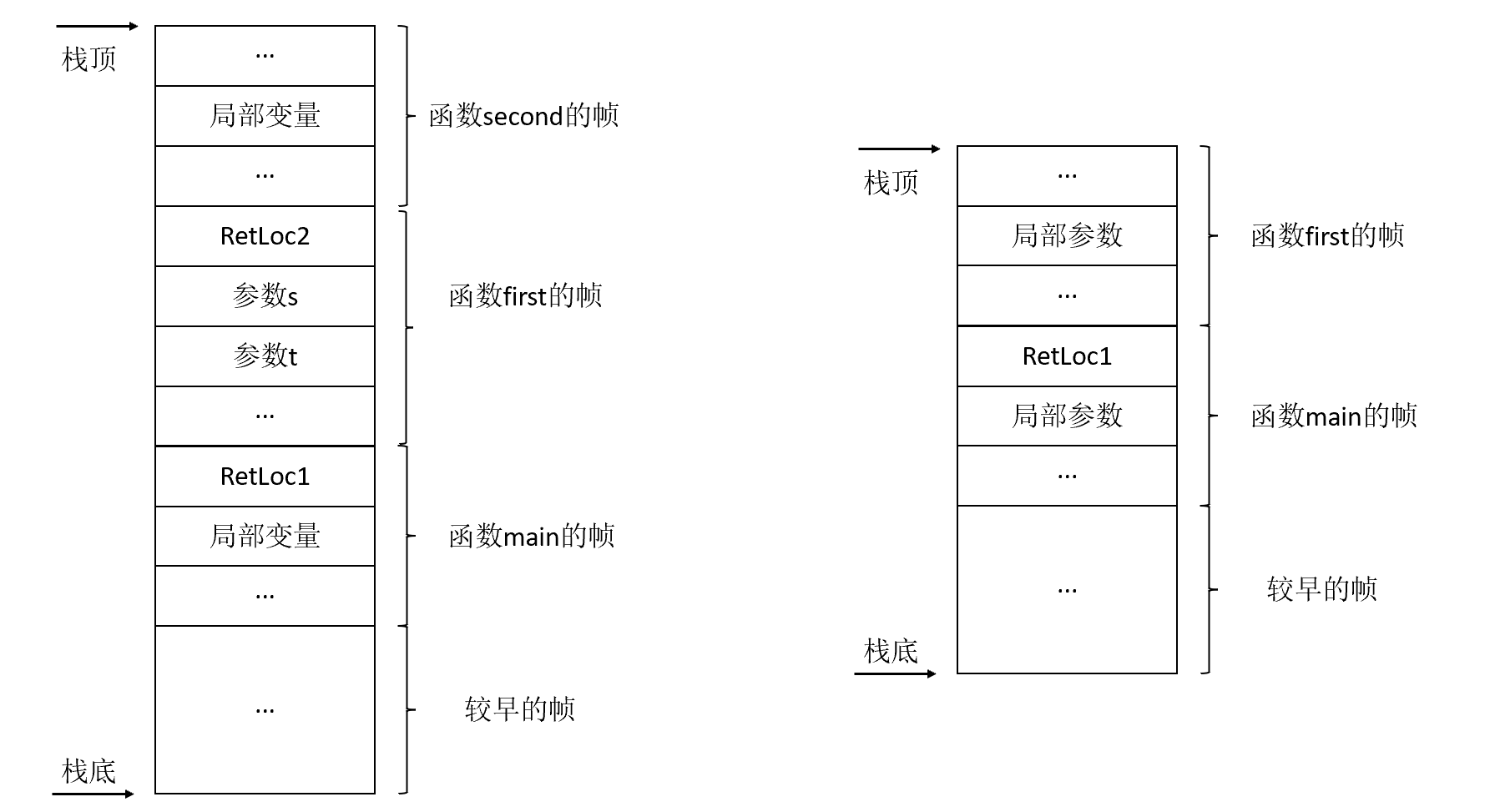
4.2.2、递归调用

递归函数的运行过程类似于多个函数的嵌套调用，只是调用函数和被调用函数是同一个函数，因此，和每次调用相关的一个重要概念是递归函数运行的“层次”。

假设调用递归函数的主函数为第0层，则从主函数调用递归函数为进入第1层；从第i层递归调用本函数为进入“下一层”，即第i+1层。反之，退出第i层递归应返回至“上一层”，即第i−1层。

为了保证递归函数正确执行，系统需设立一个“递归工作栈”作为整个递归函数运行期间使用的数据存储区。每一层递归所需信息构成一个工作记录，其中包括所有的实参、所有的局部变量，以及上一层的返回地址。每进入一层递归，就产生一个新的工作记录压入栈顶。每退出一层递归，就从栈顶弹出一个工作记录，则当前执行层的工作记录必是递归工作栈栈顶的工作记录，称这个记录为“活动记录”。

下面以阶乘函数Fact(4)为例，介绍递归过程中递归工作栈和活动记录的使用。为说明方便起见，将算法改写为：

long Fact(long n) {
    long temp;
    
    if(n==0) return 1;
    // 这里假设调用Fact(n-1)之后的返回地址为RetLoc2
    else temp=n*Fact(n-1);
    
    return temp;
}

void main() {
    long n;
    // 这里假设调用Fact(4)之后的返回地址为RetLoc1
    n=Fact(4);
}

主函数执行后依次启动了5个函数调用。如下图，为每次函数调用时活动记录的进栈情况。主程序main()调用Fact(4)的活动记录在栈底，Fact (1)调用Fact (0)进栈的活动记录在栈顶。

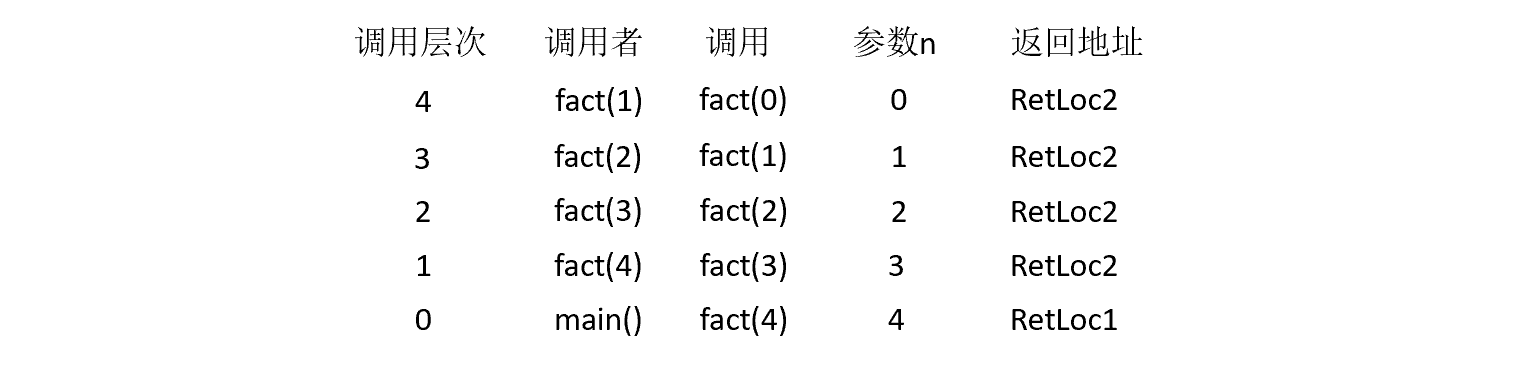
递归结束条件出现于函数Fact(0)的内部，执行Fact(0)引起了返回语句的执行。退出栈顶的活动记录，根据返回地址，返回到上一层Fact(1)的调用递归处，继续执行语句temp=1*1，接着执行return temp又引起新的退栈操作。此退栈过程直至Fact(4)执行完毕后，将控制权转移给main为止，该过程如下所示：

最后，当递归调用结束后，控制返回到RetLoc1，在此处n被赋值为24。

4.3、递归算法的效率分析

4.3.1、时间复杂度分析

迭代法是求解递归方程的一种常用方法，其基本步骤是迭代地展开递归方程的右端，使之成为一个非递归的和式，然后通过对和式的估计来达到对方程左端（即方程的解）的估计。下面，以阶乘的递归函数Fact(n)为例，说明如何通过迭代法求解递归方程来计算递归函数的时间复杂度。

假设Fact(n)的执行时间是T(n)。在该递归函数中，语句if(n==0) return 1;的执行时间是O(1)，递归调用Fact(n-1)的执行时间是T(n-1)，所以else return n*Fact(n-1);的执行时间是O(1)+T(n-1)。其中，设两数相乘和赋值操作的执行时间为O(1)。则可以得出如下递归方程（其中C、D均常数）：

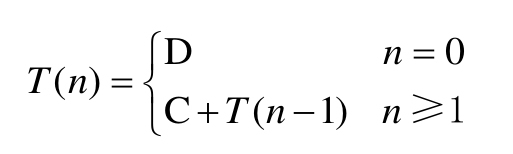
设n>2，利用上式对T(n-1)展开，即在上式中用n-1代替n，可得到：

T(n-1) = C + T(n-2)

将其带入T(n)=C+T(n-1)中，则有：

T(n) = 2C + T(n-2)

同理，当n>3时，有：

T(n) = 3C + T(n-3)

以此类推，当n>i时，有：

T(n) = iC + T(n-i)

最后，当i=n时，有

T(n) = nC + T(0) = nC + D

综上，求得阶乘的递归函数Fact(n)的时间复杂度为：T(n) = O(n)。采用这种方法计算Hanoi塔问题递归算法的时间复杂度为O(2^n^)。

4.3.2、空间复杂度分析

递归函数在执行时，系统需设立一个“递归工作栈”存储每一层递归所需的信息，此工作栈是递归函数执行的辅助空间，因此，分析递归算法的空间复杂度需要分析工作栈的大小。对于递归算法，其空间复杂度为：

S(n)=O(f(n))

其中，f(n)为“递归工作栈”中工作记录的个数与问题规模n的函数关系。根据这种分析方法不难得到，前面讨论的阶乘问题、Hanoi塔问题的递归算法的空间复杂度均为O(n)。

4.4、利用栈将递归转换为非递归的方法

对于一般的递归过程，仿照递归算法执行过程中递归工作栈的状态变化可直接写出相应的非递归算法。这种利用栈消除递归过程的步骤如下。

• 设置一个工作栈存放递归工作记录（包括实参、返回地址及局部变量等）。

• 进入非递归调用入口（即被调用程序开始处）将调用程序传来的实参和返回地址入栈（递归程序不可以作为主程序，因而可认为初始是被某个调用程序调用）。

• 进入递归调用入口：当不满足递归结束条件时，逐层递归，将实参、返回地址及局部变量入栈，这一过程可用循环语句来实现——模拟递归分解的过程。

• 递归结束条件满足，将到达递归出口的给定常数作为当前的函数值。

• 返回处理：在栈不空的情况下，反复退出栈顶记录，根据记录中的返回地址进行题意规定的操作，即逐层计算当前函数值，直至栈空为止——模拟递归求值过程。

通过以上步骤，可将任何递归算法改写成非递归算法。但改写后的非递归算法和原来比较起来，结构不够清晰，可读性差，有的还需要经过一系列的优化。

五、总结

栈是一种操作受限的线性表，它只能在表尾进行插入和删除操作。栈最大的特点是后进先出，因此栈也被称为LIFO表。栈有两种存储结构，分别是顺序栈和链栈，在顺序栈中要留意栈空和栈满的判断。栈的一个重要应用是在程序设计语言中实现递归。

六、参考

《数据结构（C语言版 第2版）》

《数据结构 自考02331》

《数据结构与算法之美》