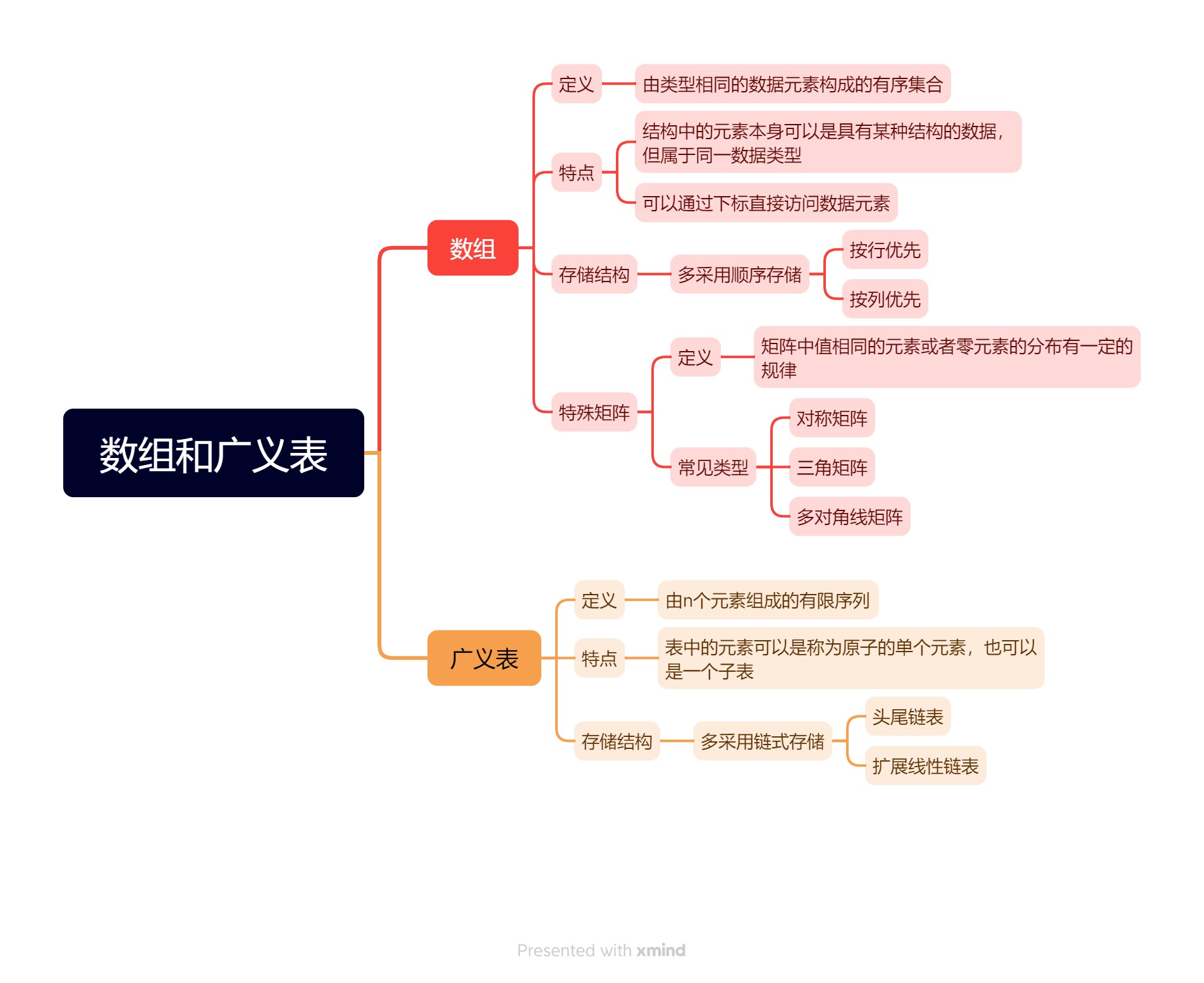
数据结构：数组和广义表

之前讨论的线性结构，比如顺序表、链表、栈、队列和字符串，表中的元素都只能是单个数据元素，而不能是具有某种结构的数据。其实，在众多的数据结构中，还有一类线性结构其数据元素可以是具有某种结构的数据。比如，我们今天要讨论的数组和广义表，它们都可以看成是对线性表的一种扩充。

一、数组

1.1、定义

数组是由类型相同的数据元素构成的有序集合。数组中的每个元素受n（n>=1）个线性关系的约束，每个元素在n个线性关系中的序号 $i_1$ ， $i_2$ ，…， $i_n$ 称为元素的下标，可以通过下标访问数据元素。因为数组中每个元素处于n（n≥1）个线性关系中，故又称数组为n维数组。

数组可以看成是线性表的推广，其特点是结构中的元素本身可以是具有某种结构的数据，但属于同一数据类型。例如，一维数组可以看成是一个线性表，二维数组可以看成数据元素是线性表的线性表。下图所示的二维数组，

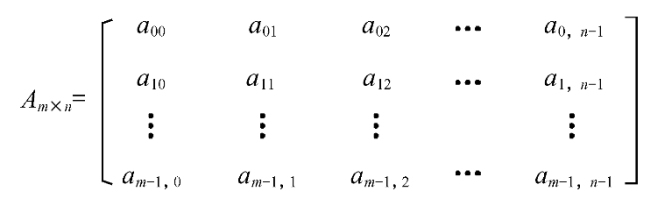
不仅可以看成是，一个行向量形式的线性表，每个数据元素 $a_i$ 为：

a_i=(a_{i0},a_{i1},...,a_{i,n-1}) \quad 0<=i<m-1

还可以看成是，一个列向量形式的线性表，每个数据元素 $a_j$ 为：

a_j=(a_{0j},a_{1j},...,a_{m-1,j}) \quad 0<=j<n-1

在C语言中，一个二维数组类型可以定义为其分量类型为一维数组的一维数组，也就是说，

1	`typedef ElemType Array2[m][n];`

等价于：

1 2	`typedef ElemType Array1[n]; typedef Array1 Array2[m];`

同理，一个n维数组类型可以定义为其数据元素为n−1维数组的一维数组。

1.2、存储结构

数组一般不做插入或删除操作，也就是说，一旦建立了数组，则结构中的数据元素个数和元素之间的关系就不再发生变动。因此，采用顺序存储结构表示数组比较合适。

存储单元是一维结构，而数组的结构可能是多维的，因此用一组连续存储单元存放数组的元素存在次序问题。通常地，对二维数组可有两种存储方式，一种是以行序为主序的存储方式：

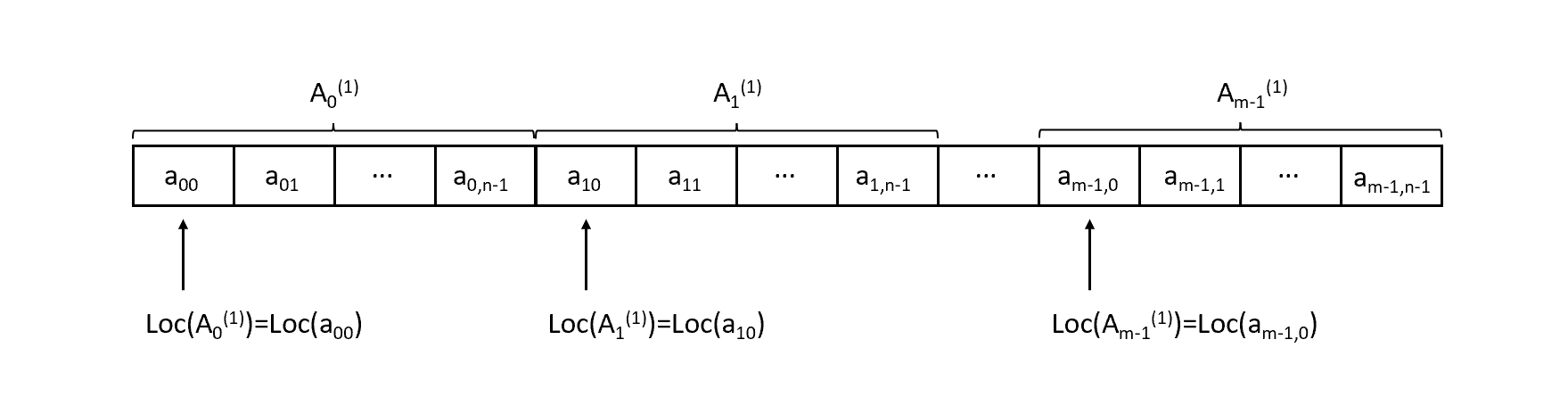
另一种是以列序为主序的存储方式：

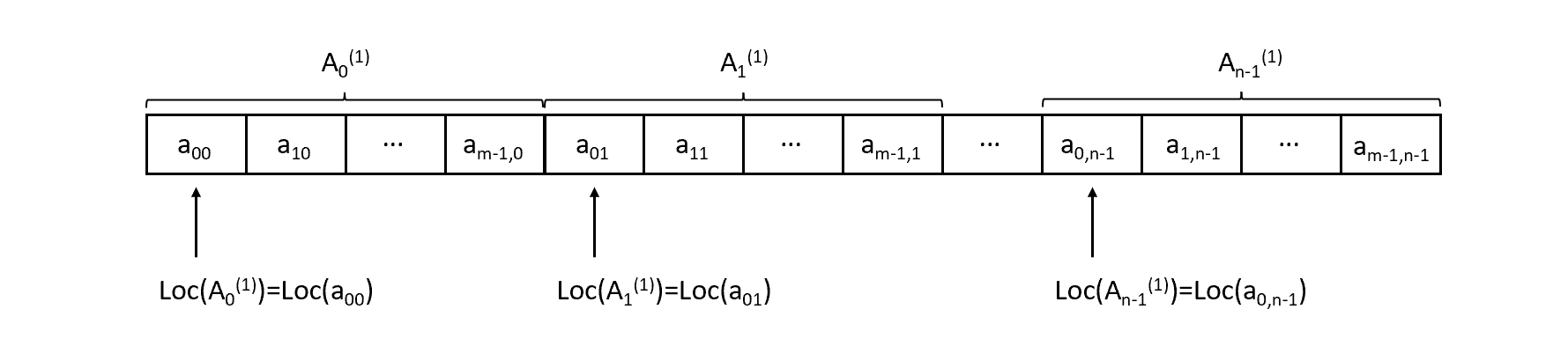
对于数组，一旦规定了其维数和各维的长度，便可为其分配存储空间。反之，只要给出一组下标便可求得相应数组元素的存储位置。以行序为主序的存储结构为例。假设，数组中每个数据元素占L个存储单元，则二维数组A[m−1][n−1]（下标从0开始，共有m行n列）中任一元素 $a_{ij}$ 的存储位置可由下式确定：

Loc(i,j)= Loc(0,0) + (n*i+j)*L

其中，Loc(i,j)是数组元素 $a_{ij}$ 的存储位置；Loc(0,0)是数组元素 $a_{00}$ 的存储位置，即二维数组A的起始存储位置，也称为基地址或基址。

1.3、特殊矩阵的压缩存储

矩阵是科学与工程计算问题中经常研究的数学对象，矩阵用二维数组来表示是最自然的方法。在数值分析中，经常出现一些阶数很高的矩阵，同时在矩阵中会有很多值相同的元素或者零元素。为了节省存储空间，可以对这类特殊矩阵进行压缩存储。

特殊矩阵，是指矩阵中值相同的元素或者零元素的分布有一定规律。特殊矩阵主要包括对称矩阵、三角矩阵和对角矩阵等。

所谓压缩存储，是指为多个值相同的元素只分配一个存储空间，对零元不分配空间。

1.3.1、对称矩阵

对于n阶对称矩阵来说，矩阵中的元满足下述性质：

a_{ij}=a_{ji} \quad(1<=i,j<=n)

在n阶对称矩阵中，可为每一对对称元分配一个存储空间，即可将 $n^2$ 个元压缩存储到n(n+1)/2个元的空间中。

不失一般性，以行序为主序存储其下三角（包括对角线）中的元。假设以一维数组sa[n(n+1)/2]作为n阶对称矩阵的存储结构，则sa[k]和矩阵 $a_{ij}$ 之间，存在如下对应关系：

k = \begin{cases} \frac{i(i-1)}{2}+j-1\quad当i>=j\quad(元位于下三角) \\ \frac{j(j-1)}{2}+i-1\quad当i<j\quad(元位于上三角) \end{cases}

对于任意给定的一组下标(i,j)，均可在sa中找到矩阵元 $a_{ij}$ ；反之，对所有的k=0，1，2，…， $\frac{n(n+1)}{2}-1$ ，都能确定sa[k]中的元在矩阵中的位置(i,j)。由此，称sa[n(n+1)/2]为n阶对称矩阵的压缩存储。

1.3.2、三角矩阵

以主对角线划分，三角矩阵有上三角矩阵和下三角矩阵两种。上三角矩阵是指矩阵下三角（不包括对角线）中的元均为常数c或零的n阶矩阵，下三角矩阵则与之相反。对三角矩阵进行压缩存储时，除了和对称矩阵一样，只存储其上（下）三角中的元素之外，再加一个存储常数c的存储空间即可。

在下三角矩阵中，sa[k]和矩阵元 $a_{ij}$ 之间的对应关系为：

k = \begin{cases} \frac{i(i-1)}{2}+j-1\quad当i>=j\quad(元位于下三角) \\ \frac{n(n+1)}{2}\quad当i<j\quad(元位于上三角) \end{cases}

在上三角矩阵中，sa[k]和矩阵元 $a_{ij}$ 之间的对应关系为：

k = \begin{cases} \frac{n(n+1)}{2}\qquad当i>j\quad(元位于下三角) \\ \frac{(i-1)(2n-i+2)}{2}+j-i\quad当i<=j\quad(元位于上三角) \end{cases}

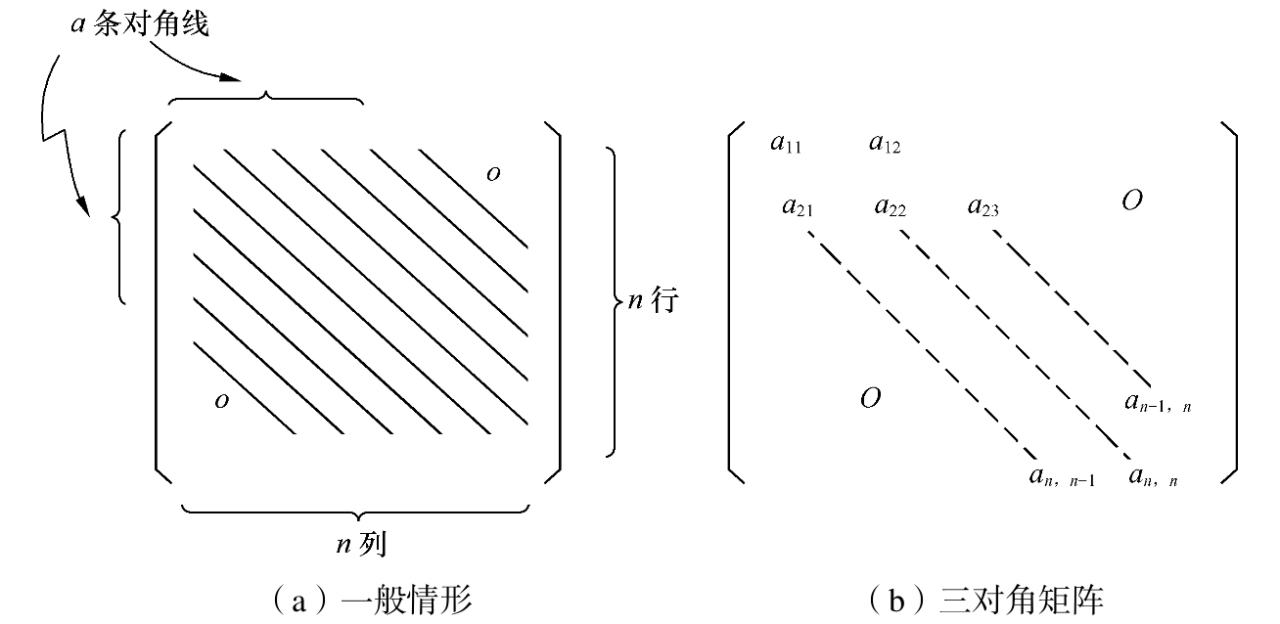
1.3.3、多对角线矩阵

在多对角线矩阵中，所有非零元都集中在以主对角线为中心的带状区域中，即除了主对角线上和主对角线上、下方若干条对角线上的元之外，所有其他的元皆为零，如下图所示。

1.4、稀疏矩阵的压缩存储

稀疏矩阵，是指矩阵中非零元素的个数远小于矩阵元素的总数。

为了节省存储单元，对于稀疏矩阵，也可用压缩存储方法，只存储非零元素。

稀疏矩阵中的非零元素一般是没有规律的。在存储非零元素时，除了存储非零元素的值之外，还必须同时存储该元素的行、列位置（即下标）。因此，可用一个三元组 $(i,j,a_{ij})$ 来唯一确定一个非零元素。

当用三元组来表示非零元素时，对稀疏矩阵进行压缩存储通常有两种方法：顺序存储和链式存储。链式存储一般采用的是十字链表法，结构比较复杂。这里只介绍顺序存储方式的压缩存储技术。

1.4.1、三元组表

如果将表示稀疏矩阵非零元素的三元组按行优先的顺序排列，则可得到一个其结点均为三元组的线性表，即三元组表。

为了操作方便，对稀疏矩阵的总行数、总列数以及非零元素个数均作为三元组表的辅助属性加以描述。在C语言中，三元组表的类型定义如下：

// 假设非零元素个数的最大值为1000个
#define MaxSize 1000

// 三元组类型
typedef struct {
  // 非零元素的行号、列号（即下标）
  int i,j;
  // 非零元素值
  DataType v;
}TriTupleNode;

// 稀疏矩阵类型
typedef struct {
  // 存储三元组的数组
  TriTupleNode data[MaxSize];
  // 矩阵的行数、列数和非零元素个数
  int m,n,t;
}TSMatrix;

1.4.2、带行表的三元组表

为了便于随机存取任意一行的非零元素，可在按行优先存储的三元组表中，增加一个存储每一行的第一个非零元素在三元组表中位置的数组。这样就得到稀疏矩阵的另一种存储结构——带行表的三元组表，又称为行逻辑链接的顺序表。在C语言中，其类型描述如下：

typdef struct {
  TriTupleNode data[MaxSize];
  int m,n,t;
  // 每行第一个非零元素的位置表
  int RowPos[MaxRow];
}RLSMatrix;

二、广义表

广义表，也称列表，它是线性表的推广。线性表的元素仅限于原子项，即每个数据元素只能是一个数或一个记录，如果放松对线性表的这种限制，允许它们自身具有结构，由此就产生了广义表的概念。广泛地用于人工智能等领域的表处理语言——LISP语言，把广义表作为基本的数据结构，就连程序也表示为一系列的广义表。

2.1、定义

广义表是由n个元素组成的有限序列，一般记作

LS=(a_1,a_2,...,a_n)

其中，LS是广义表( $a_1$ , $a_2$ ,…, $a_n$ )的名称，n是其长度。在线性表中， $a_i$ (1<=i<=n)只能是单个元素；而在广义表中， $a_i$ 可以是单个元素，也可以是广义表，它们分别称为广义表LS的原子和子表。习惯上，用大写字母表示广义表的名称，用小写字母表示原子。

广义表的定义是一个递归的定义，因为在描述广义表时又用到了广义表。如下，是一些广义表的例子。

A=()，A是一个空表，其长度为0。
B=(e)，B只有一个原子e，其长度为1。
C=(a, (b, c, d))，C的长度为2，两个元素分别为原子a和子表(b, c, d)。
D=(A, B, C)，D的长度为3，3个元素都是广义表。显然，将子表的值代入后，则有D=((), (e), (a, (b, c, d)))。
E=(a, E)，E的长度为2，它是一个递归表，相当于一个无限的广义表E=(a, (a, (a, …)))。

从上述定义和例子，可推出广义表的如下3个重要结论。

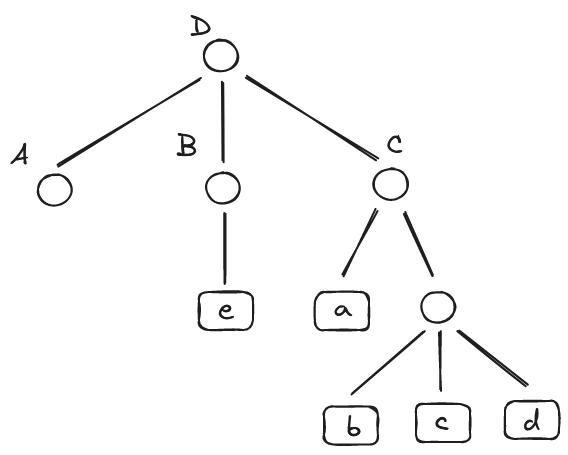
广义表的元素可以是子表，而子表的元素还可以是子表……由此，广义表是一个多层次的结构，可以用图形象地表示。例如，下图表示的是广义表D，图中以圆圈表示广义表，以方块表示原子。
广义表可为其他广义表所共享。例如，在上述例子中，广义表A、B和C为D的子表，则在D中可以不必列出子表的值，而是通过子表的名称来引用。
广义表可以是一个递归表，即广义表也可以是其本身的一个子表。例如，表E就是一个递归表。

2.2、基本运算

由于广义表的结构比较复杂，因此其各种运算的实现，没有线性表那么简单。其中，最重要的几个运算如下。

取表头GetHead(LS)：取出的表头是，非空广义表的第一个元素，它可以是一个单原子，也可以是一个子表。
取表尾GetTail(LS)：取出的表尾是，除去表头之外，其余元素构成的表，即表尾一定是一个广义表。
求长度Length(LS)：广义表的长度是其元素个数。
求深度Depth(LS)：广义表的深度是其最大层次数减1。

例如：

GetHead(B)=e
GetTail(B)=()
Length(B)=1
Depth(B)=1
GetHead(D)=A
GetTail(D)=(B, C)
Length(D)=3
Depth(D)=3

由于(B, C)为非空广义表，因此可继续分解得到：

GetHead(B, C)=B
GetTail(B, C)=(C)

这里需要注意的是，广义表( )和(( ))不同。前者为空表，长度n=0；后者长度n=1，可分解得到其表头、表尾均为空表( )。

2.3、存储结构

由于广义表中的数据元素可以有不同的结构（或是原子，或是列表），因此难以用顺序存储结构表示，通常采用链式存储结构。常用的链式存储结构有两种，头尾链表的存储结构和扩展线性链表的存储结构。

2.3.1、头尾链表的存储结构

由于广义表中的数据元素可能为原子或广义表，因此需要两种结构的结点：一种是原子结点，用以表示原子；一种是表结点，用以表示广义表。其中，一个原子结点由2个域组成：标志域和值域；一个表结点由3个域组成：标志域、指示表头的指针域和指示表尾的指针域。它们的结构如下图所示，其中tag是标志域，值为0时表示结点是原子，值为1时表示结点是子表。对于一个非空的广义表来说，它可以被分解成表头和表尾，因此，一对确定的表头和表尾可唯一确定广义表。

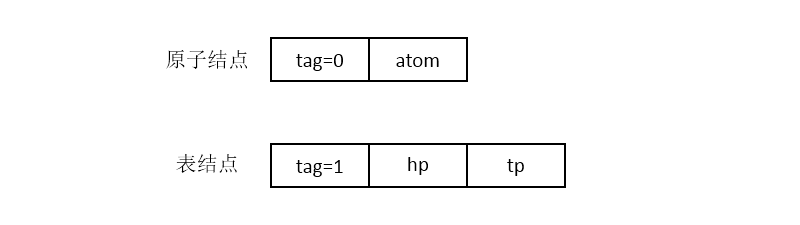
在C语言中，广义表的头尾链表存储结构的类型描述如下：

// ATOM==0:原子
// LIST==1:子表
typedef enum{ATOM,LIST} ElemTag;

// 广义表类型
typedef struct GLNode {
    // 公共部分，用于区分原子结点和表结点
    ElemTag tag;
    
    // 原子结点和表结点的联合部分
    union {
        // atom是原子结点的值域，AtomType由用户定义
        AtomType atom;
        // ptr是表结点的指针域，ptr.hp和ptr.tp分别指向表头和表尾
        struct {
            struct GLNode *hp, *tp;
        }ptr;
    };
}*GList;

前面列举的广义表的例子，它们的头尾链表存储结构是这样的：

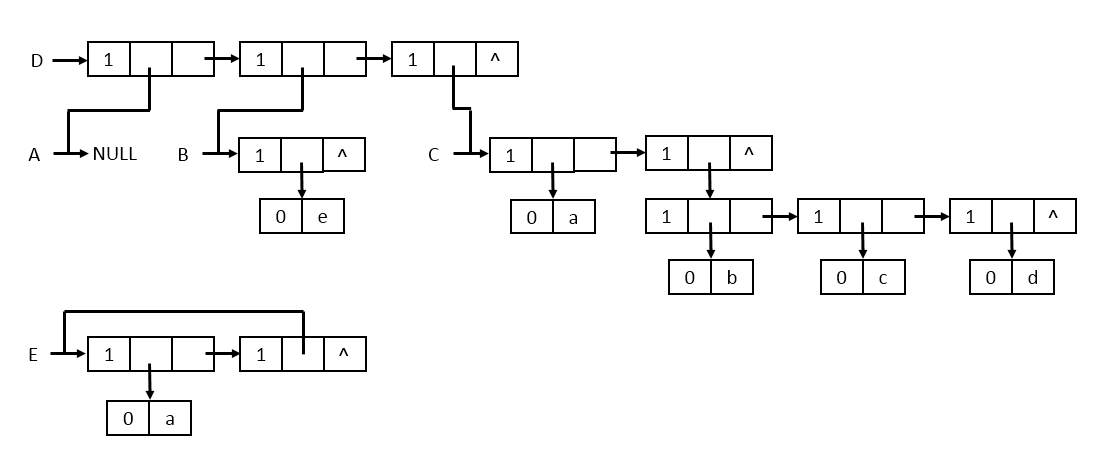
说明：

除空表的表头指针为空外，对于任何非空广义表来说，其表头指针均指向一个表结点，且该结点中的hp域指示广义表表头（或为原子结点，或为表结点），tp域指向广义表表尾（除非表尾为空，则指针为空，否则必为表结点）。
在这种存储结构中，易分清广义表中原子和子表所在层次。比如，在广义表D中，原子a和e在同一层次上，而b、c和d在同一层次且比a和e低一层，B和C是同一层的子表。
最高层的表结点个数即为广义表的长度。

2.3.2、扩展线性链表的存储结构

在这种结构中，无论是原子结点还是表结点均由三个域组成，其结点结构如下图所示：

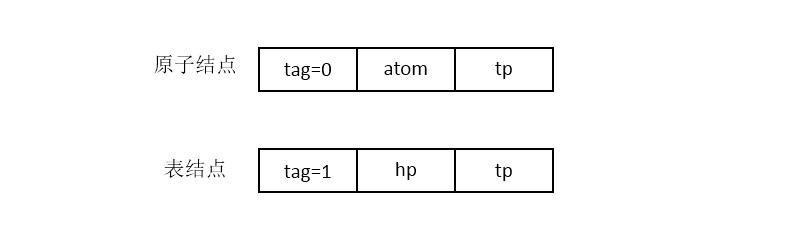
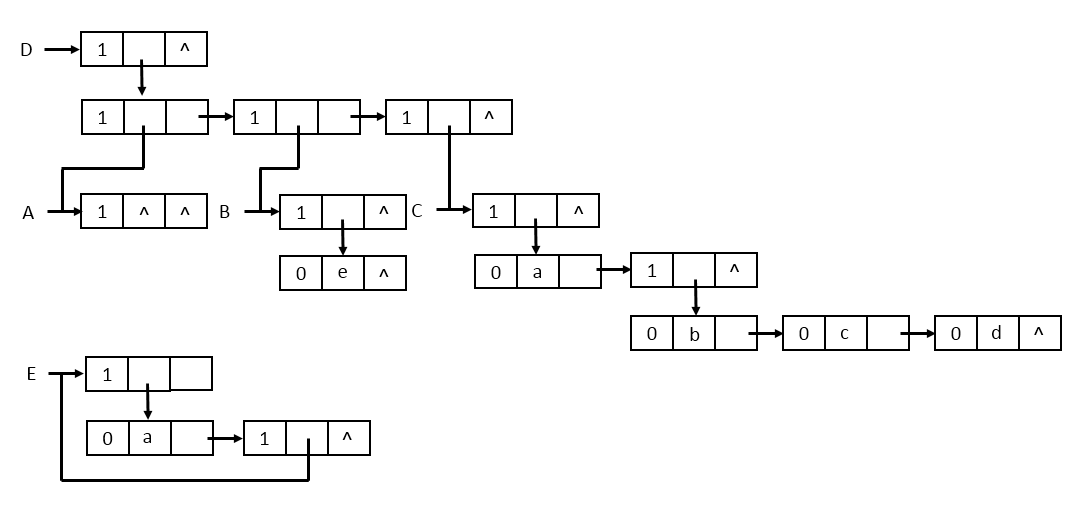
前面列举的广义表的例子，它们的扩展线性链表存储结构是这样的：

三、小结

数组可以看成是线性表的推广，其特点是结构中的元素本身可以是具有某种结构的数据，但属于同一数据类型。一个n维数组实质上是n个线性表的组合，其每一维都是一个线性表。数组一般采用顺序存储结构，因为物理存储是一维的，故存储多维数组时，应先将其转换为一维结构（按行转换或按列转换）。科学与工程计算中的矩阵通常用二维数组来表示，为了节省存储空间，对于几种常见形式的特殊矩阵，比如对称矩阵、三角矩阵和对角矩阵，在存储时可进行压缩存储，即为多个值相同的元只分配一个存储空间，对零元不分配空间。

广义表是另一种线性表的推广形式，表中的元素可以是称为原子的单个元素，也可以是一个子表。线性表可以看成广义表的特例，表中的元素都是称为原子的单个元素。。广义表的结构相当灵活，在某种前提下，它可以兼容线性表、数组、树和有向图等各种常用的数据结构。广义表的常用操作有取表头和取表尾。广义表通常采用链式存储结构：头尾链表的存储结构和扩展线性链表的存储结构。

四、参考

《数据结构（C语言版第2版）》

《数据结构自考02331》

数据结构

#数据结构

数据结构：数组和广义表

https://kuberxy.github.io/2023/12/31/数据结构06：数组和广义表/

作者

Mr.x

发布于

2023年12月31日

许可协议

数据结构：树的基本概念上一篇

数据结构：字符串下一篇