数据结构：图的遍历

和树的遍历类似，图的遍历也是从图中某一顶点出发，按照某种方法对图中所有顶点访问且仅访问一次。图的遍历算法是求解图的连通性问题、拓扑排序和关键路径等算法的基础。

一、图的遍历问题

图的遍历要比树的遍历复杂得多。图中任一顶点都可能和其余顶点相邻接。在访问了某个顶点之后，可能沿着某条路径搜索又回到该顶点上。例如，下图所示的无向图，由于图中存在回路，因此在访问了 $v_1、v_2、v_3、v_4$ 之后，沿着边 $(v_4,v_1)$ 又可访问到 $v_1$ 。

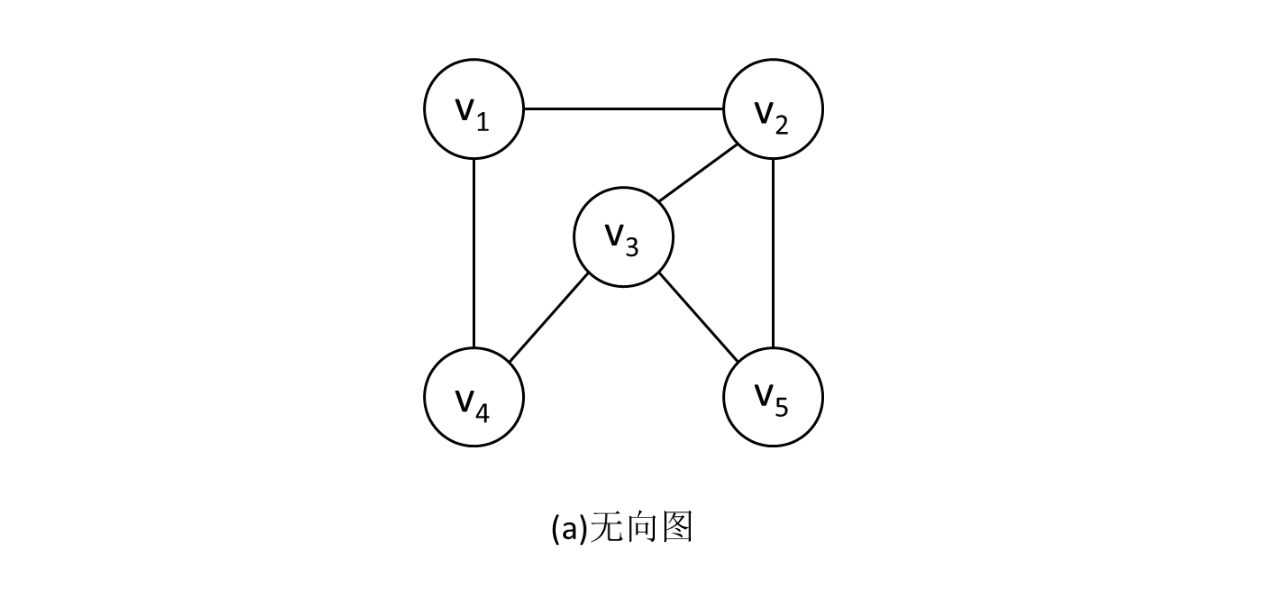
为了避免同一顶点被访问多次，在遍历图的过程中，必须记下每个已访问过的顶点。为此，可以设置一个辅助数组visited[n]，其初始值置为“false”或者0，一旦访问了顶点 $v_i$ ，便置visited[i]为“true”或者1。

图的遍历方法有很多，但常用的有两种，根据搜索路径的方向分为：深度优先搜索和广度优先搜索。它们对无向图和有向图都适用。

二、深度优先搜索

2.1、搜索过程

深度优先搜索（Depth First Search，DFS）类似于树的先序遍历。对于一个连通图，深度优先搜索的过程如下：

从图中某个顶点v出发，访问v。
找出顶点v的第一个未被访问的邻接点，访问该顶点。以该顶点作为新的v，重复此步骤，直至顶点v没有未被访问的邻接点为止。
返回至前一个访问过的、且仍有邻接点未被访问的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点，将该顶点作为新的v。
重复第二步和第三步，直至图中所有顶点都被访问过，搜索结束。

如下图，图（b）是图（a）所示无向图的深度优先搜索过程。在图（b）中，带箭头的实线表示遍历时的访问路径，带箭头的虚线表示遍历时的回溯路径。

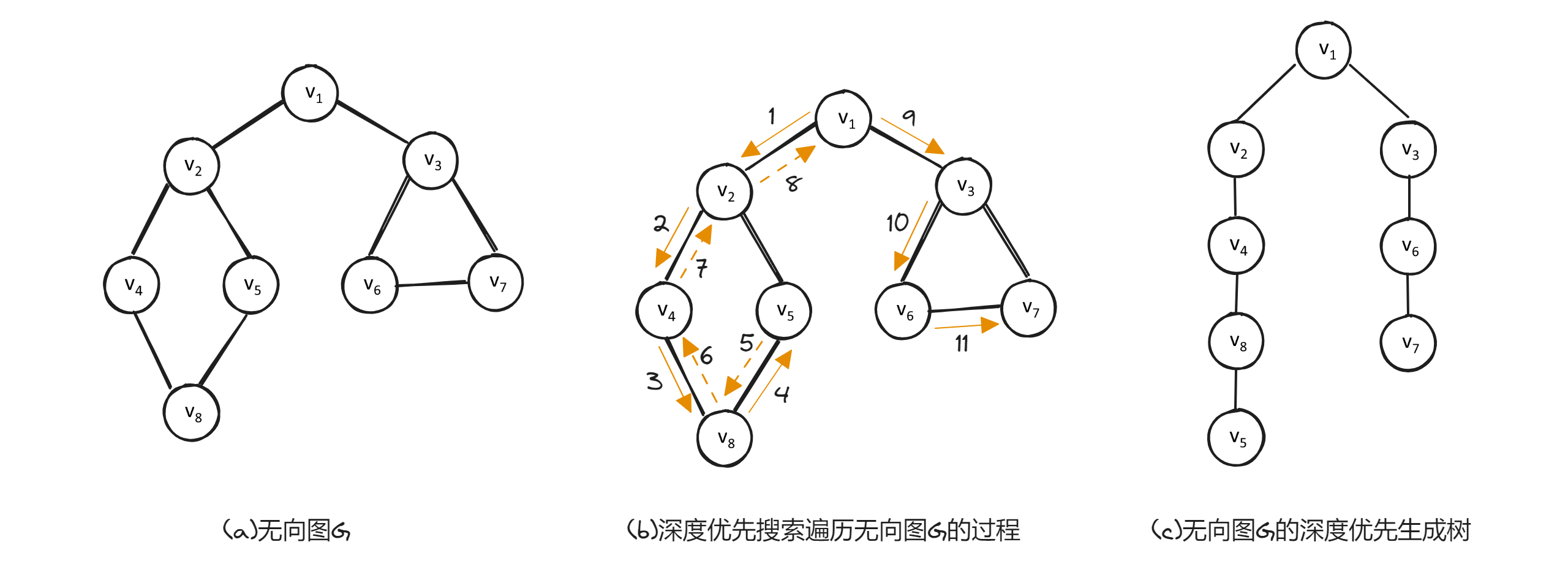
使用深度优先搜索，遍历上图（a）所示的无向图，具体过程如下：

从顶点 $v_1$ 出发，访问 $v_1$ 。
找出 $v_1$ 的第一个未被访问的邻接点 $v_2$ ，访问 $v_2$ 。以 $v_2$ 为新顶点，重复该步骤，先后访问 $v_4、v_8、v_5$ 。访问 $v_5$ 后，由于 $v_5$ 的邻接点都已被访问，此步骤结束。
搜索从 $v_5$ 回到 $v_8$ ，由于同样的理由，搜索继续回到 $v_4、v_2$ 直至 $v_1$ ，此时由于 $v_1$ 的另一个邻接点未被访问，则搜索又从 $v1$ 到 $v3$ ，再继续下去。由此，得到的顶点访问序列为： $v_1 \longrightarrow v_2 \longrightarrow v_4 \longrightarrow v_8 \longrightarrow v_5 \longrightarrow v_3 \longrightarrow v_6 \longrightarrow v_7$

深度优先搜索遍历最终会得到一棵以 $v_1$ 为根的树，称之为深度优先生成树，其形式如上图（c）所示。

2.2、算法实现

深度优先搜索遍历连通图是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问，需附设访问标志数组visited[n]，其初值为“false”，一旦某个顶点被访问，则其相应的分量置为“true”。

深度优先搜索遍历连通图的算法步骤为：

从图中某个顶点v出发，访问v，并置visited[v]的值为true。
依次检查v的所有邻接点w，如果visited[w]的值为false，则再从w出发进行递归遍历，直到图中所有顶点都被访问过。

相应的算法描述为：

// 访问标志数组，其初值为false
bool visited[MVNum]

// 从第v个顶点出发深度优先遍历图G
void DFS(Graph G, int v) {
    // 访问第v个顶点，并置访问标志数组相应分量值为true
    cout<<v;
    visited[v]=true;
    // 依次检查v的所有邻接点w
    // FirstAdjVex(G, v)表示v的第一个邻接点
    // NextAdjVex(G,v,w)表示v相对于w的下一个邻接点
    // w>=0表示存在邻接点
    for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
        // 对v的尚未访问的邻接点w递归调用DFS()
        if(!visited[w]) DFS(G,w);
}

若是非连通图，上述遍历过程执行之后，图中一定还有顶点未被访问。因此，需要从图中另选一个未被访问的顶点作为起始点，重复上述深度优先搜索过程，直到图中所有顶点均被访问过为止。这样，要实现对非连通图的遍历，就需要循环调用上述算法。深度优先搜索遍历非连通图的算法描述为：

// 对非连通图G做深度优先遍历
void DFSTraverse(Graph G) {
    // 初始化标志数组
    for(v=0;v<G.vexnum;++v)
        visited[v]=false;

    // 对尚未访问的顶点调用DFS
    for(v=0;v<G.vexnum;++v)
        if(!visited[v]) DFS(G,v);
}

该算法每调用一次DFS算法将遍历一个连通分量，由多少次调用，就说明图中有多少个连通分量。

2.3、算法分析

在遍历图时，对图中每个顶点至多调用一次DFS函数，因为一旦某个顶点被标志成已被访问，就不再从它出发进行搜索。因此，遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间则取决于所采用的存储结构。

当用邻接矩阵表示图时，查找每个顶点的邻接点的时间复杂度为 $O(n^2)$ ，其中n为图中顶点数。而当以邻接表做图的存储结构时，查找邻接点的时间复杂度为O(e)，其中e为图中边数。由此，当以邻接表做存储结构时，深度优先搜索遍历图的时间复杂度为O(n+e)。

三、广度优先搜索

3.1、搜索过程

广度优先搜索（Breadth First Search，BFS）类似于树的按层次遍历。广度优先搜索的过程如下：

从图中某个顶点v出发，访问v。
依次访问v的所有未曾访问过的邻接点。
将这些邻接点分别作为新的v，并依次访问它们的邻接点。访问过程中，使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。重复此步骤，直至图中所有已被访问的顶点的邻接点都被访问到。

如下图，图（b）是图（a）所示无向图的广度优先搜索过程。

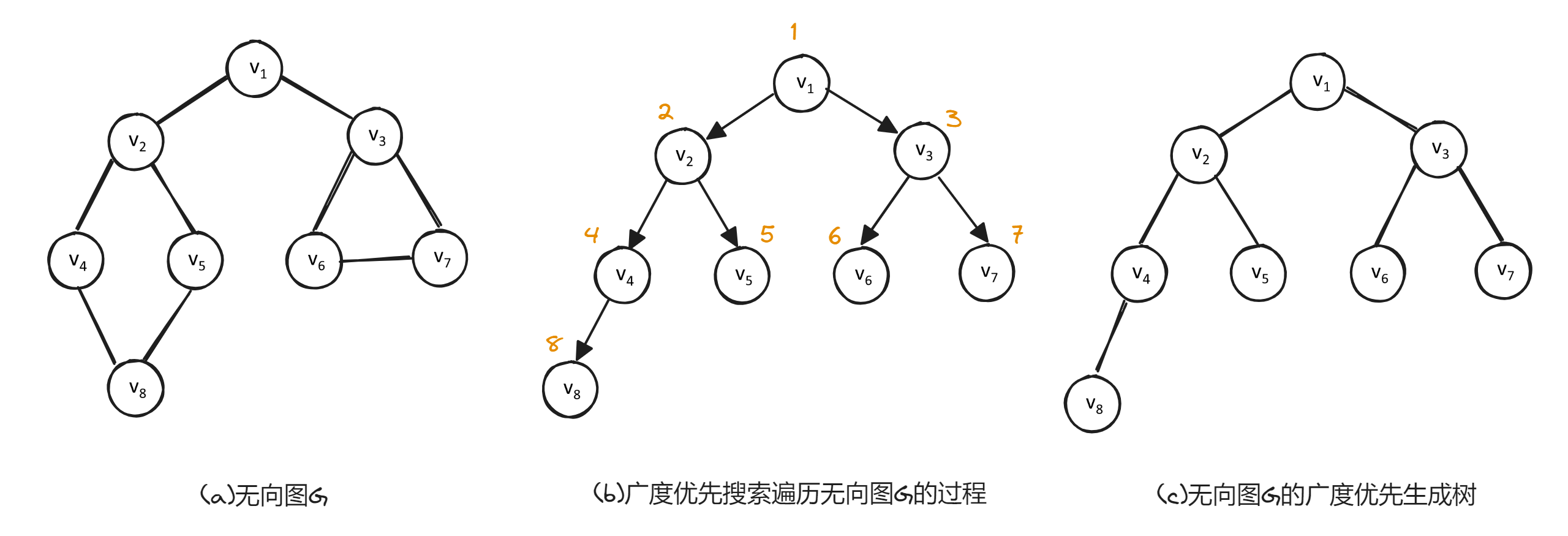
具体过程如下：

首先，从顶点 $v_1$ 出发，访问 $v_1$ 。
然后，依次访问 $v_1$ 的各个未曾访问过的邻接点 $v_2$ 和 $v_3$ 。
接着，依次访问 $v_2$ 的邻接点 $v_4$ 和 $v_5$ ，以及 $v_3$ 的邻接点 $v_6$ 和 $v_7$ 。
最后，访问 $v_4$ 的邻接点 $v_8$ 。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问了，由此完成了图的遍历。得到的顶点访问序列为： $v_1 \longrightarrow v_2 \longrightarrow v_3 \longrightarrow v_4 \longrightarrow v_5 \longrightarrow v_6 \longrightarrow v_7 \longrightarrow v_8$

广度优先搜索，最终也会构成一棵以 $v_1$ 为根的树，称之为广度优先生成树。其形式如上图（c）所示。

可以看出，广度优先搜索的特点是：尽可能先进行横向搜索。设x和y是两个相继被访问过的顶点，若当前是以x为出发点进行搜索，则在访问了x的所有未曾被访问过的邻接点后，紧接着是以y为出发点进行横向搜索，并对搜索到的y的邻接点中尚未被访问的顶点进行访问。

3.2、算法实现

在广度优先搜索中，先访问的顶点其邻接点亦先被访问。为此，实现算法时需引进队列，保存已被访问过的顶点。和深度优先搜索类似，广度优先搜索在遍历的过程中，也需要一个访问标志数组。广度优先搜索遍历连通图的算法步骤为：

从图中某个顶点v出发，访问v，并置visited[v]的值为true，然后将v进队。
只要队列非空，则重复下述操作：
- 队头元素u出队；
- 依次检查u的所有邻接点w，如果visited[w]的值为false，则访问w，并置visited[w]的值为true，然后使w入队。

相应算法描述为：

// 按广度优先遍历连通图G
void BFS(Graph G, int v) {
    // 访问第v个顶点，并置访问标志数组相应分量值为true
    count<<v;
    visited[v]=true;

    // 初始化队列Q
    InitQueue(Q);
    // v进队
    EnQueue(Q,v);

    // 队列非空
    while(!QueueEmpty(Q)) {
        // 队头元素出队并置为u
        DeQueue(Q,u);
        // 依次检查u的所有邻接点w
        // FirstAdjVex(G,u)表示u的第一个邻接点
        // NextAdjVex(G,u,w)表示u相对于w的下一个邻接点
        // w>=0表示存在邻接点
        for(FirstAdjVex(G,u);w>=0;w=NextAdjVex(G,u,w)) {
            // w为u的尚未访问的邻接点
            if(!visited[w]) {
                // 访问w，并置访问标志数组相应分量值为true
                count<<w;
                visited[w]=true;
                // w进队
                EnQueue(Q,w)
            }
        }
    }
}

若是非连通图，上述遍历过程执行之后，图中一定还有顶点未被访问，需要从图中另选一个未被访问的顶点作为起始点，重复上述广度优先搜索过程，直到图中所有顶点均被访问过为止。该算法的实现类似于深度优先搜索遍历非连通图的算法，仅需将算法中的DFS函数调用改为BFS函数调用。

3.3、算法分析

每个顶点至多进一次队列。遍历图的过程实质上是通过边找邻接点的过程，因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同，即当用邻接矩阵存储时，时间复杂度为 $O(n^2)$ ；用邻接表存储时，时间复杂度为O(n+e)。

四、小结

图的遍历算法是实现图的其他运算的基础，图的遍历方法有两种：深度优先搜索遍历和广度优先搜索遍历。深度优先搜索遍历类似于树的先序遍历，借助于栈结构来实现（递归）；广度优先搜索遍历类似于树的层次遍历，借助于队列结构来实现。两种遍历方法的不同之处仅仅在于对顶点访问的顺序不同，所以时间复杂度相同。当用邻接矩阵存储时，时间复杂度为均 $O(n^2)$ ，用邻接表存储时，时间复杂度均为O(n+e)。