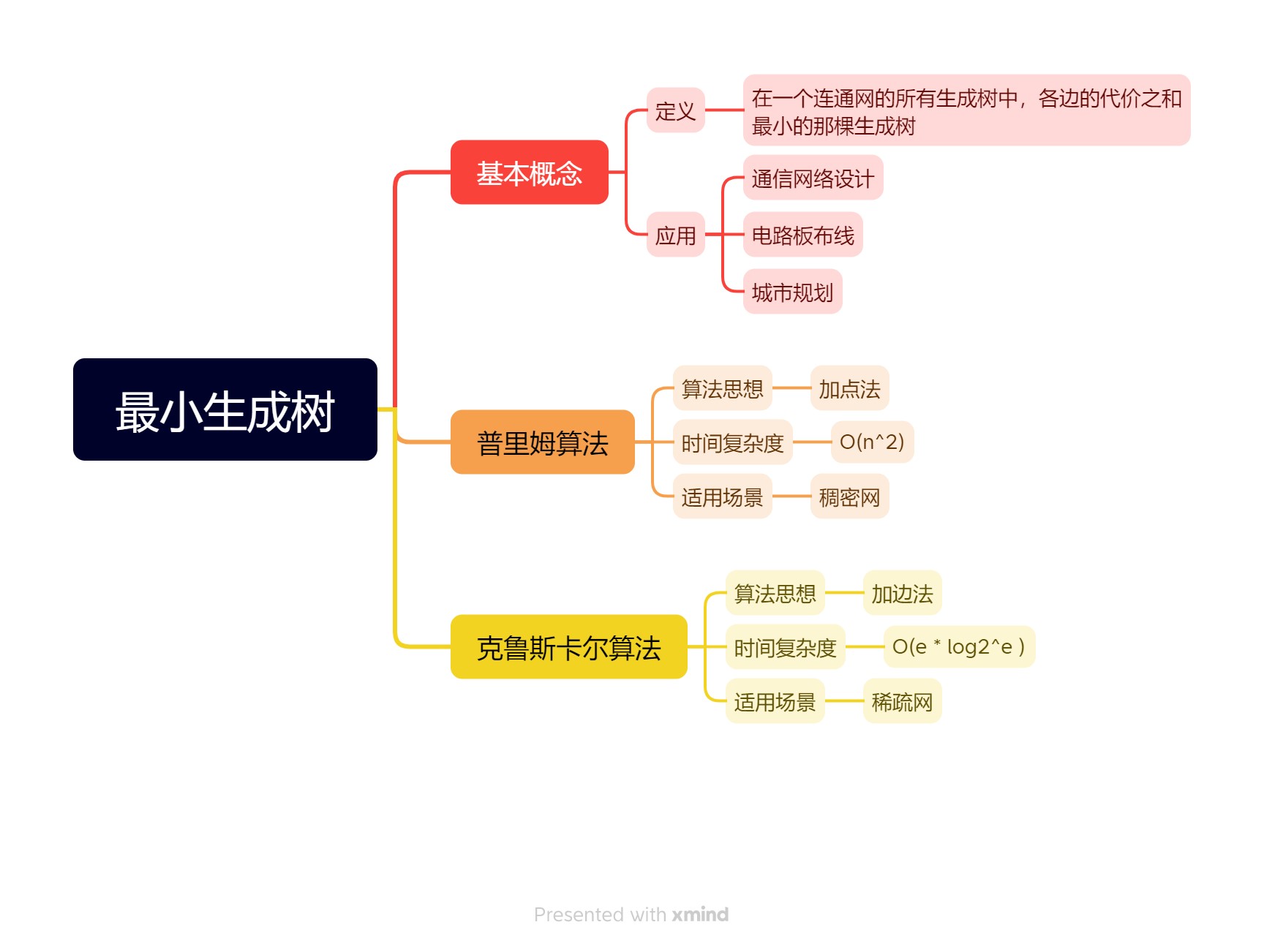
数据结构：最小生成树

最小生成树是图论中的一个重要概念，它在许多实际应用中都扮演着重要角色，比如通信网络设计、电路板布线、城市规划等。在实际应用中，最小生成树的构建可以帮助优化网络设计、资源分配等问题。通过选择最小生成树，可以在保持网络连通性的前提下，使得整体成本最小化。因此，了解最小生成树的概念和算法对于解决实际问题具有重要意义。

一、基本概念

在一个连通网的所有生成树中，各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树（Minimum Cost Spanning Tree），简称为最小生成树。

假设要在n个城市之间建立通信联络网，则连通n个城市只需要n−1条线路。这时，自然会考虑这样一个问题，如何在最节省经费的前提下建立这个通信网。

在每两个城市之间都可设置一条线路，相应地都要付出一定的经济代价。n个城市之间，最多可能设置n(n−1)/2条线路，那么，如何在这些可能的线路中选择n−1条，以使总的耗费最少呢？

可以用连通网来表示n个城市，以及n个城市间可能设置的通信线路，其中网的顶点表示城市，边表示两城市之间的线路，赋予边的权值表示相应的代价。对于n个顶点的连通网可以建立许多不同的生成树，每一棵生成树都可以是一个通信网。最合理的通信网应该是代价之和最小的生成树。

构造最小生成树有多种算法，其中多数算法利用了最小生成树的一种简称为MST的性质：假设G=(V, E)是一个连通网，U是顶点集V的一个非空子集。若(u, v)是一条具有最小权值（代价）的边，其中 $u \in U, v \in V-U$ ，则必存在一棵包含边(u, v)的最小生成树。

上述性质可用反证法来证明。假设连通网G的任何一棵最小生成树都不包含(u, v)。设T是连通网上的一棵最小生成树，当将边(u, v)加入到T中时，由生成树的定义，T中必存在一条包含(u, v)的回路。另一方面，由于T是生成树，则在T上必存在另一条边(u’, v’)，其中 $u' \in U, v' \in V-U$ ，且u和u’之间、v和v’之间均有路径相同。删去边(u’, v’)，便可消除上述回路，同时得到另一棵生成树T’。因为(u, v)的权值不高于(u’, v’)，则T’的权值亦不高于T，T’是包含(u, v)的一棵最小生成树。由此和假设矛盾。

二、普里姆算法

2.1、构造过程

假设G=(V, E)是一个具有n个顶点的连通网，T=(U, TE)是G的最小生成树。

初始情况下，U和TE均为空，即U={}，TE={}。
从V中任取一个顶点（假定为 $v_1$ ），将它并入U中，此时 $U=\{v_1\}$ 。
在那些一端已在U中，另一端仍在U外的所有边中，找一条权值最小的边(u, v)，其中 $u \in U, v \in V-U$ ，将该边并入TE，同时v并入U。
重复上一步，直至U=V为止。此时，TE中必有n-1条边，则T是G的最小生成树。

如下图，是连通网G按普里姆算法构造最小生成树的过程。

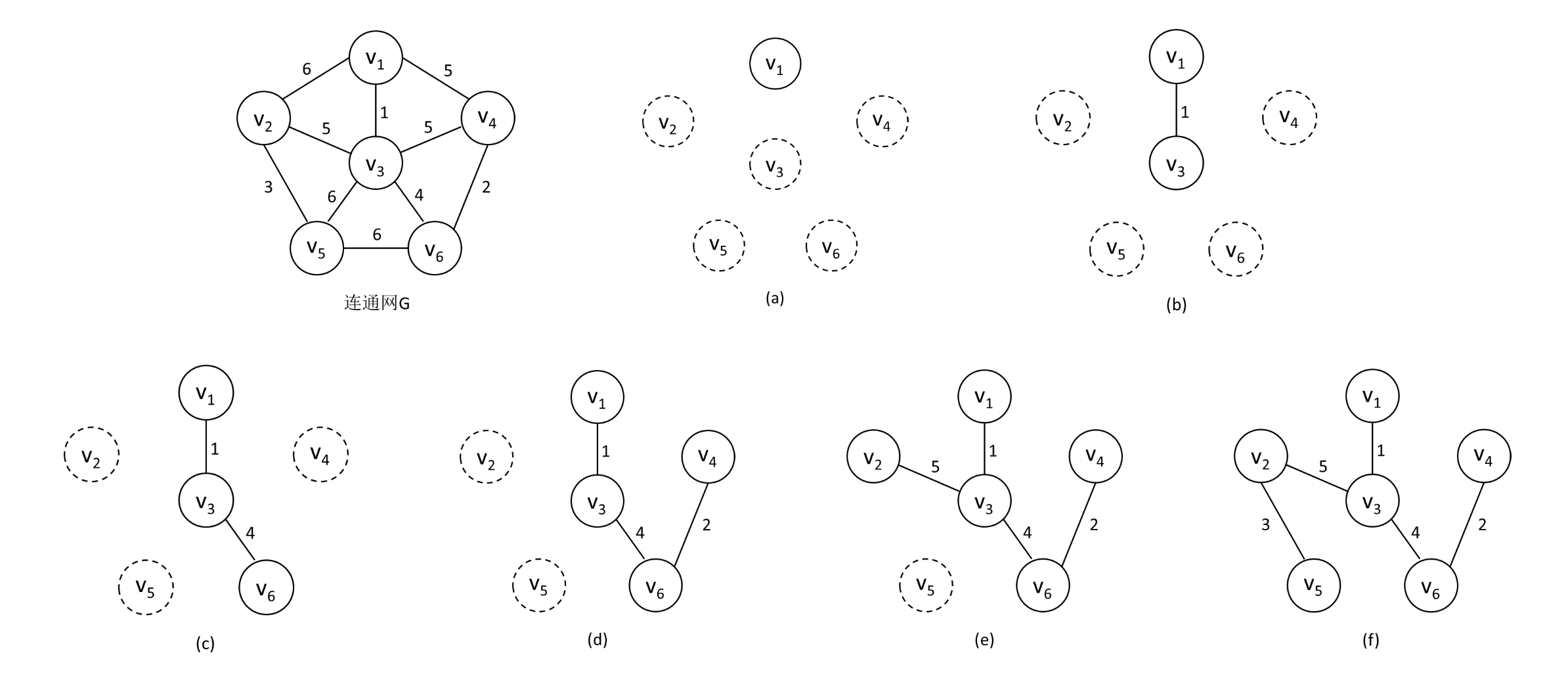
一开始 $U=\{v_1\}$ ，然后在所有从U到V-U的边中，找到一条权值最小的边 $(v_1,v_3)$ 并入TE，并将 $v_3$ 并入U，此时 $U=\{v_1, v_3\}$ ；接着继续在所有从U到V-U的边中，找到一条权值最小的边 $(v_3,v_6)$ 并入TE，并将 $v_6$ 并入U，此时 $U=\{v_1, v_3, v_6\}$ ；依此类推，直到U=V。

可以看出，普里姆算法逐步增加U中的顶点，因此可称其为“加点法”。每次选择最小边时，可能存在多条同样权值的边可选，此时任选其一即可。

2.2、算法实现

假设一个连通网G以邻接矩阵形式存储，从顶点u出发构造G的最小生成树T，要求输出T的各条边。

为实现这个算法需附设一个辅助数组closedge，以记录从U到V−U具有最小权值的边。对每个顶点 $v_i \in V-U$ ，在辅助数组中存在一个相应分量closedge[i-1]，它包括两个域：lowcost和adjvex，其中lowcost存储最小边上的权值，adjvex存储最小边在U中的那个顶点。也即 $closedge[i-1].lowcost=Min\{cost(u, v_i)|u \in U\}$ ，其中cost(u, v)表示赋于边(u, v)的权。在C语言中，辅助数组closedge的定义如下：

// 辅助数组的定义，用来记录从顶点集U到V-U的权值最小的边
struct {
    VerTexType adjvex;
    ArcType lowcost;
}closedge[MVNum];

普里姆算法的步骤如下：

首先将初始顶点u并入U中，对其余的每一个顶点 $v_j$ ，将closedge[j]初始化为到u的边信息。
循环n-1次，选择其余的n-1个顶点，生成n-1条边：
- 从closedge中选出权值最小的边closedge[k]，输出此边；
- 将k并入U中；
- 更新closedge信息，由于新顶点的加入，从U到V-U会有新边，如果新边的权值比closedge[j].lowcost小，则将closedge[j]更新为新边。

相应的算法描述为：

void MiniSpanTree_Prim(AMGraph G, VerTexType u) {
    // k为顶点u的下标
    k=LocateVex(G,u)
    // 初始U={u}
    closedge[k].lowcost=0;
    // 对V-U中的每一个顶点vj，初始化closedge[j]
    for(j=0;j<G.vernum;++j)
        // closedge[j]={adjvex, lowcost} 
        if(j!=k) closedge[j]={u, G.arcs[k][j]}

    // 选择其余n-1个顶点，生成n-1条边(n=G.vexnum)
    for(i=1;i<G.vexnum;++i) {
        // 求出U的下一个顶点: 第k个顶点，closedge[k]中存有当前权值最小的边
        k=Min(closedge);
        // u0为最小边的一个顶点，u0属于U
        u0=closedge[k].adjvex;
        // v0为最小边的另一个顶点，v0属于V−U
        v0=G.vexs[k];
        // 输出当前的最小边(u0, v0) 
        cout << u0 << v0;
        // 第k个顶点并入U
        closedge[k].lowcost=0;
        // 新顶点并入U后更新closedge
        for(j=0;j<G.vernum;++j)
            if(G.arcs[k][j]<closedge[j].lowcost)
                closedge[j]={G.vexs[k],G.arcs[k][j]}
    }
}

假设网中有n个顶点，则第一个进行初始化的循环语句的频度为n，第二个循环语句的频度为n−1。其中，第二个循环语句中有两个内循环：其一是在closedge[v].lowcost中求最小值，其频度为n−1；其二是重新选出具有最小权值的边，其频度为n。由此，普里姆算法的时间复杂度为 $O(n^2)$ ，与网中的边数无关，因此适用于求稠密网的最小生成树。

下表是利用普里姆算法对前面的连通网G从顶点 $v_1$ 开始构造最小生成树各量的变化。

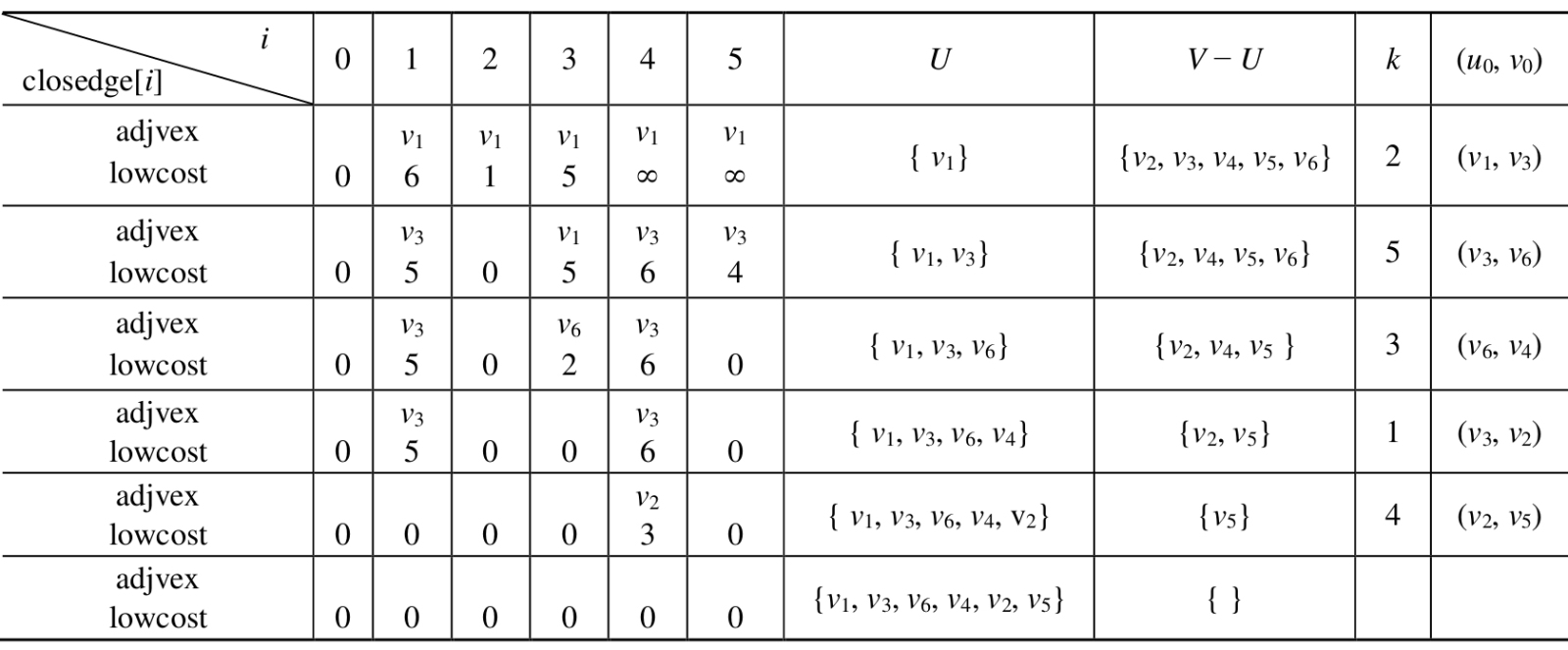
初始状态时， $U=\{v_1\}$ ，从U到V−U具有最小权值的边，就是从依附于顶点 $v_1$ 的各条边中，找到一条权值最小的边 $(v_1,v_3)$ 为生成中的第一条边，同时将顶点 $v_3$ 并入集合U中。然后修改辅助数组中的值，首先将closedge[2].lowcost改为0，表明顶点 $v_3$ 已并入U。又由于边 $(v_3,v_2)$ 的权值小于closedge[1].lowcost，则需修改closedge[1]为边 $(v_3,v_2)$ 及其权值。同理修改closedge[4]和closedge[5]。依次类推，直到U=V。

三、克鲁斯卡尔算法

3.1、构造过程

假设G=(V, E)是一个具有n个顶点的连通网，T=(U, TE)是G的最小生成树。

初始状态下，U=V，TG={}，即T的初始状态是只含有n个顶点而无边的非连通图T=(V, {})。
将图G中的边按权值从小到大排序。
依次选取E中的边，若选取的边使生成树T不形成回路，则把它并入TE中，否则将其舍弃。
重复上一步，直到TE中包含n-1条边为止，此时的T即为最小生成树。

如下图，是连通网G按克鲁斯卡尔算法构造最小生成树的过程。

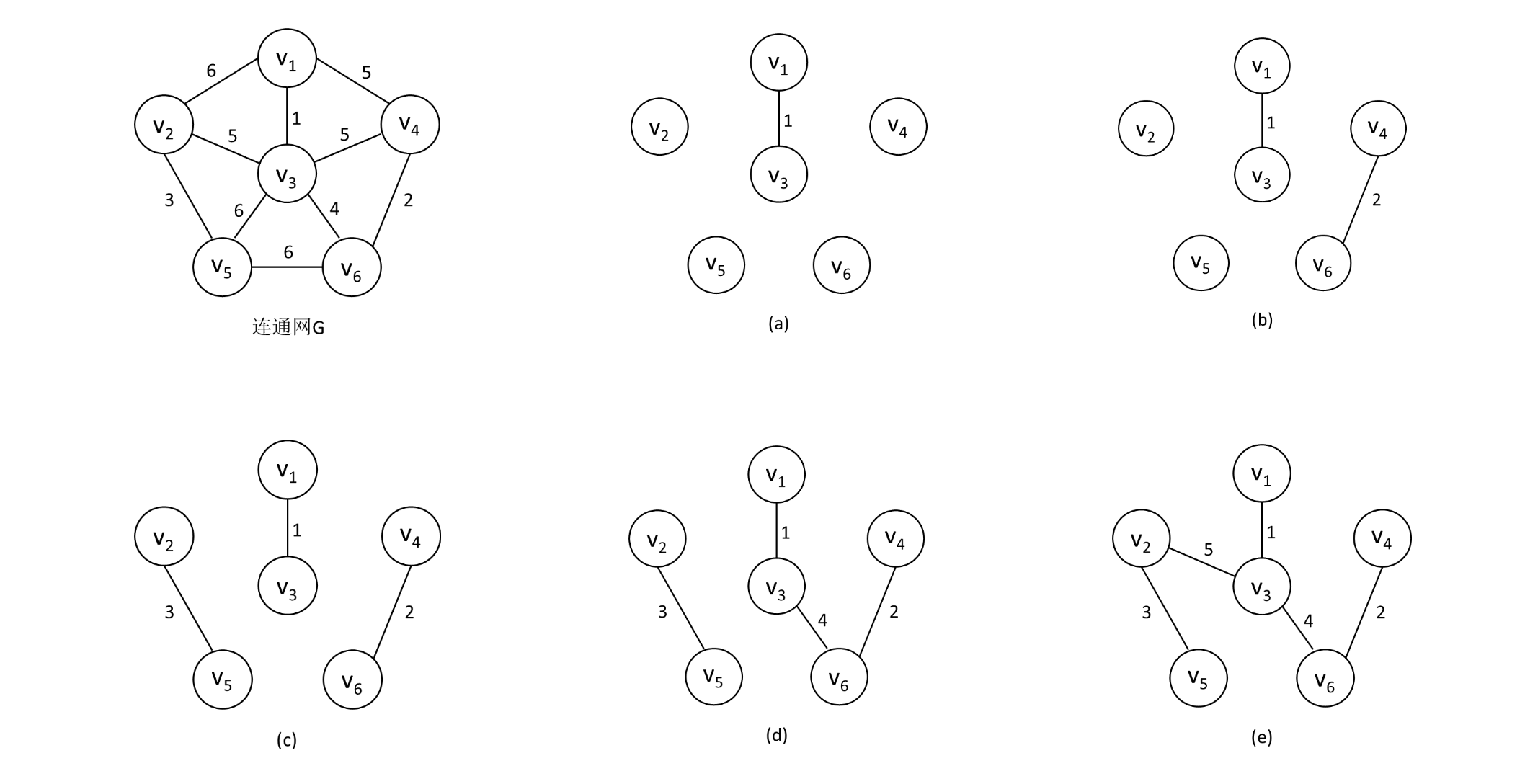
权值分别为1、2、3、4的4条边由于满足上述条件，则先后被加入到T中；权值为5的两条边 $(v_1,v_4)$ 和 $(v_3,v_4)$ 被舍去，因为它们依附的两顶点在同一连通分量上，它们若加入T 中，则会使T产生回路，而另一条权值为5的边 $(v_2,v_3)$ 连接两个连通分量，则可加入T 。由此，构造成一棵最小生成树。

可以看出，克鲁斯卡尔算法逐步增加生成树的边，与普里姆算法相比，可称为“加边法”。与普里姆算法一样，每次选择最小边时，可能有多条同样权值的边可选，可以任选其一。

3.2、算法实现

克鲁斯卡尔算法的实现需要引入以下辅助的数据结构：

结构体数组Edge：存储边的信息，包括边的两个顶点和权值。
数组Vexset，标识各个顶点所属的连通分量。对每个顶点 $v_i \in V$ ，在辅助数组中存在一个相应元素Vexset[i]表示该顶点所在的连通分量。初始时Vexset[i]=i，表示自成一个连通分量。

在C语言中，上述辅助数据结构的定义如下：

// 结构体数组Edge
struct {
    // 边的始点
    VerTexType Head;
    // 边的终点
    VerTexType Tail;
    // 边上的权值
    ArcType lowcost;
}Edge[arcnum];

// 数组Vexset
int Vexset[MVNum];

克鲁斯卡尔算法的步骤为：

将数组Edge中的元素按权值从小到大排序。
依次查看数组Edge中的边，循环执行以下操作：
- 依次从排好序的数组Edge中选出一条边 $(v_1,v_2)$ ；
- 在数组Vexset中分别查找 $v_1$ $v_{1}$ 和 $v_2$ $v_{2}$ 所在的连通分量 $vs_1$ $v s_{1}$ 和 $vs_2$ $v s_{2}$ ，并进行判断：
  - 如果 $vs_1$ 和 $vs_2$ 不等，表明所选的两个顶点分属不同的连通分量，输出此边，并合并 $vs_1$ 和 $vs_2$ 两个连通分量；
  - 如果 $vs_1$ 和 $vs_2$ 相等，表明所选的两个顶点属于同一个连通分量，舍去此边而选择下一条权值最小的边。

相应的算法描述为：

// 无向网G以邻接矩阵形式存储，构造G的最小生成树T，输出T的各条边
void MiniSpanTree_Kruskal(AMGraph G) {
    // 将数组Edge中的元素按权值从小到大排序
    Sort(Edge);
    // 初始化数组Vexset
    for(i=0;i<G.vexnum;++i) Vexset[i]=i;

    // 依次查看数组Edge中的边
    for(i=0;i<G.arcnum;++i) {
        // v1为边的始点Head的下标
        v1=LocateVex(G, Edge[i].Head);
        // v2为边的终点Tail的下标
        v2=LocateVex(G, Edge[i].Tail);
        // 获取边Edge[i]的始点所在的连通分量vs1
        vs1=Vexset[v1];
        // 获取边Edge[i]的终点所在的连通分量vs2
        vs2=Vexset[v2];
        if(vs1!=vs2) {
            // 输出此边
            cout << Edge[i].Head << Edge[i].Tail;
            // 合并vs1和vs2两个分量，即两个集合统一编号
            for(j=0;j<G.vexnum;++j)
                // 集合编号为vs2的都改为vs1
                if(Vexset[j]==vs2) Vexset[j]=vs1;
        }
    }
}

若以“堆”来存放网中的边进行堆排序，对于包含e条边的网，上述算法排序时间是 $O(e\log_{2}{e})$ 。在for循环中最耗时的操作是合并两个不同的连通分量，只要采取合适的数据结构，可以证明其执行时间为 $O(\log_{2}{e})$ ，因此整个for循环的执行时间是 $O(e\log_{2}{e})$ 。由此，克鲁斯卡尔算法的时间复杂度为 $O(e\log_{2}{e})$ ，与网中的边数有关，与普里姆算法相比，克鲁斯卡尔算法更适合于求稀疏网的最小生成树。