数据结构：树表的查找之二叉树排序

线性表的查找更适用于插入或删除操作不频繁的场景。对于插入或删除操作频繁的场景，想要进行高效率的查找，就需要使用树表，即采用树形数据结构作为查找表的组织形式，这主要包括二叉排序树、平衡二叉树、B树等。本文将重点讨论二叉排序树。

一、定义

二叉排序树（Binary Sort Tree），又称二叉查找树，是一种对排序和查找都很有用的特殊二叉树。一棵二叉排序树或是一棵空树，或是具有下列性质的二叉树：

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树。

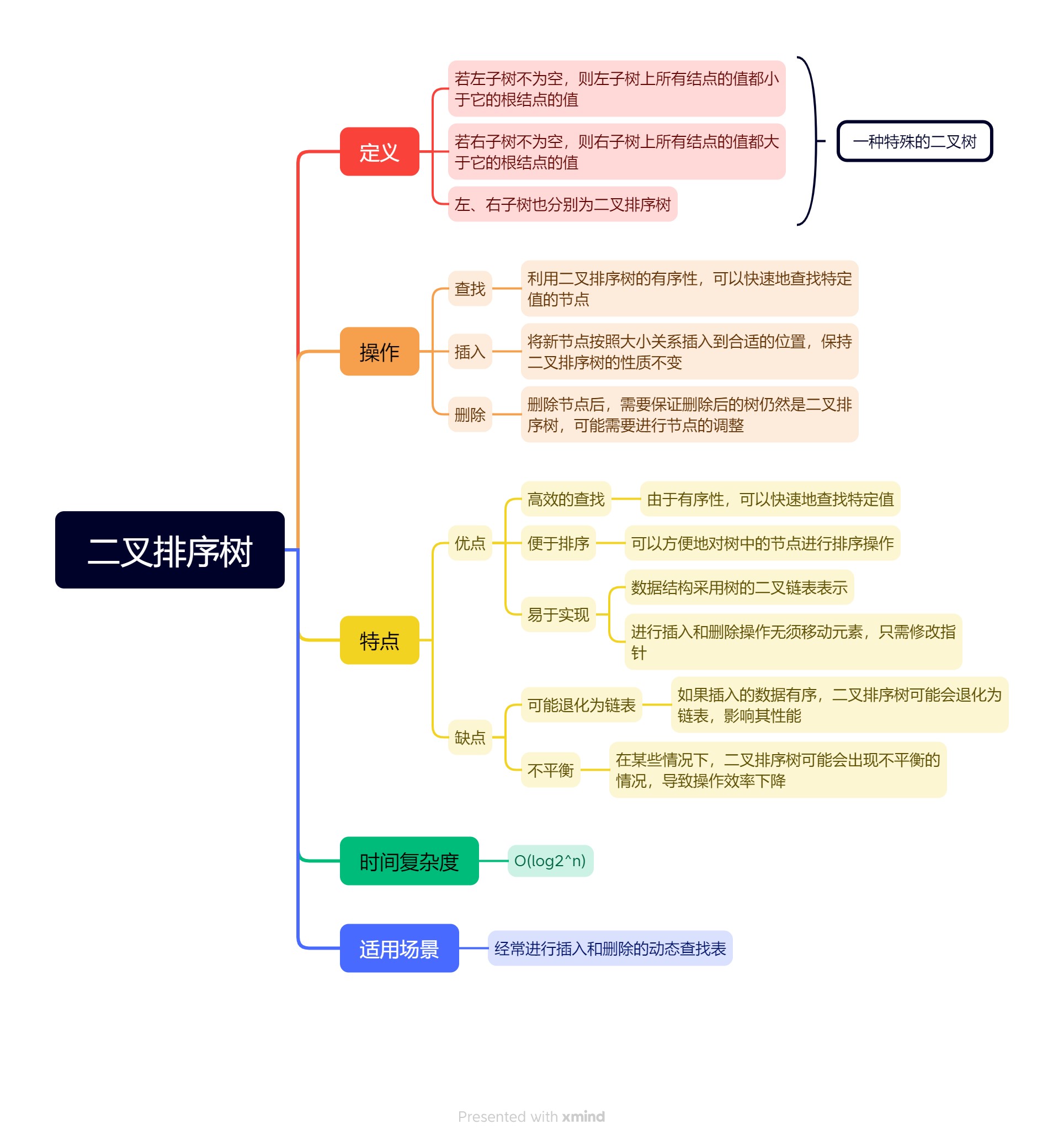
二叉排序树是递归定义的。由定义可以得出二叉排序树的一个重要性质：中序遍历一棵二叉排序树时，可以得到一个结点值递增的有序序列。例如，下图就是一棵二叉排序树。

image-20240213135134595

中序遍历这棵二叉排序树，将得到一个按数值大小排序的递增序列：

3,12,24,37,45,53,61,78,90,1003,12,24,37,45,53,61,78,90,100

下面，我们以二叉链表作为存储结构，讨论二叉排序树的各种操作。因为二叉排序树的操作要根据结点的关键字域来进行，所以下面给出了每个结点的数据域的类型定义（包括关键字项和其他数据项）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 每个结点的数据域的类型
typedef struct {
    // 关键字项
    KeyType key;
    // 其他数据项
    InfoType otherinfo;
}ElemType;

typedef struct BSTNode {
    // 每个结点的数据域包括关键字项和其他数据项
    ElemType data;
    // 左右孩子指针
    struct BSTNode *lchild,*rchild;
}BSTNode, *BSTree;

二、查找

二叉排序树可以看成是一个有序表，在二叉排序树上进行查找和折半查找类似，也是一个逐步缩小查找范围的过程。二叉排序树的递归查找算法步骤为：

  • 若二叉排序树为空，则查找失败，返回空指针。
  • 若二叉排序树非空，将给定值key与根结点的关键字T->data.key进行比较：
    • 若key等于T->data.key，则查找成功，返回根结点地址；
    • 若key小于T->data.key，则递归查找左子树；
    • 若key大于T->data.key，则递归查找右子树。

相应的算法描述为：

1
2
3
4
5
6
7
8
9
10
11
// 在根指针T所指向的二叉排序树中，递归查找关键字等于key的数据元素
// 若查找成功，则返回指向该数据元素结点的指针，否则返回空指针
BSTree SearchBST(BSTree T, KeyType key) {
    // 指针为空或找到关键字等于key的数据元素，查找结束
    if( (!T) || key==T->data.key ) return T;

    // 在左子树中继续查找
    if(key<T->data.key) SearchBST(T->lchild, key);
    // 在右子树中继续查找
    else SearchBST(T->rchild, key);
}

接下来，我们以下图为例，说明在二叉排序树中进行查找的过程：

image-20240213135134595

在这棵二叉排序树中查找关键字等于100的记录（树中结点内的数均为记录的关键字）。首先以key=100和根结点的关键字做比较，因为key>45，则查找以45为根的右子树，此时右子树不空，且key>53，则继续查找以结点53为根的右子树，由于key和53的右子树根的关键字100相等，则查找成功，返回指向结点100的指针值。

在这棵二叉排序树中查找关键字等于40的记录。和上述过程类似，在给定值key与关键字45、12及37相继比较之后，继续查找以结点37为根的右子树，此时右子树为空，则说明该树中没有待查记录，故查找不成功，返回指针值为“NULL”。

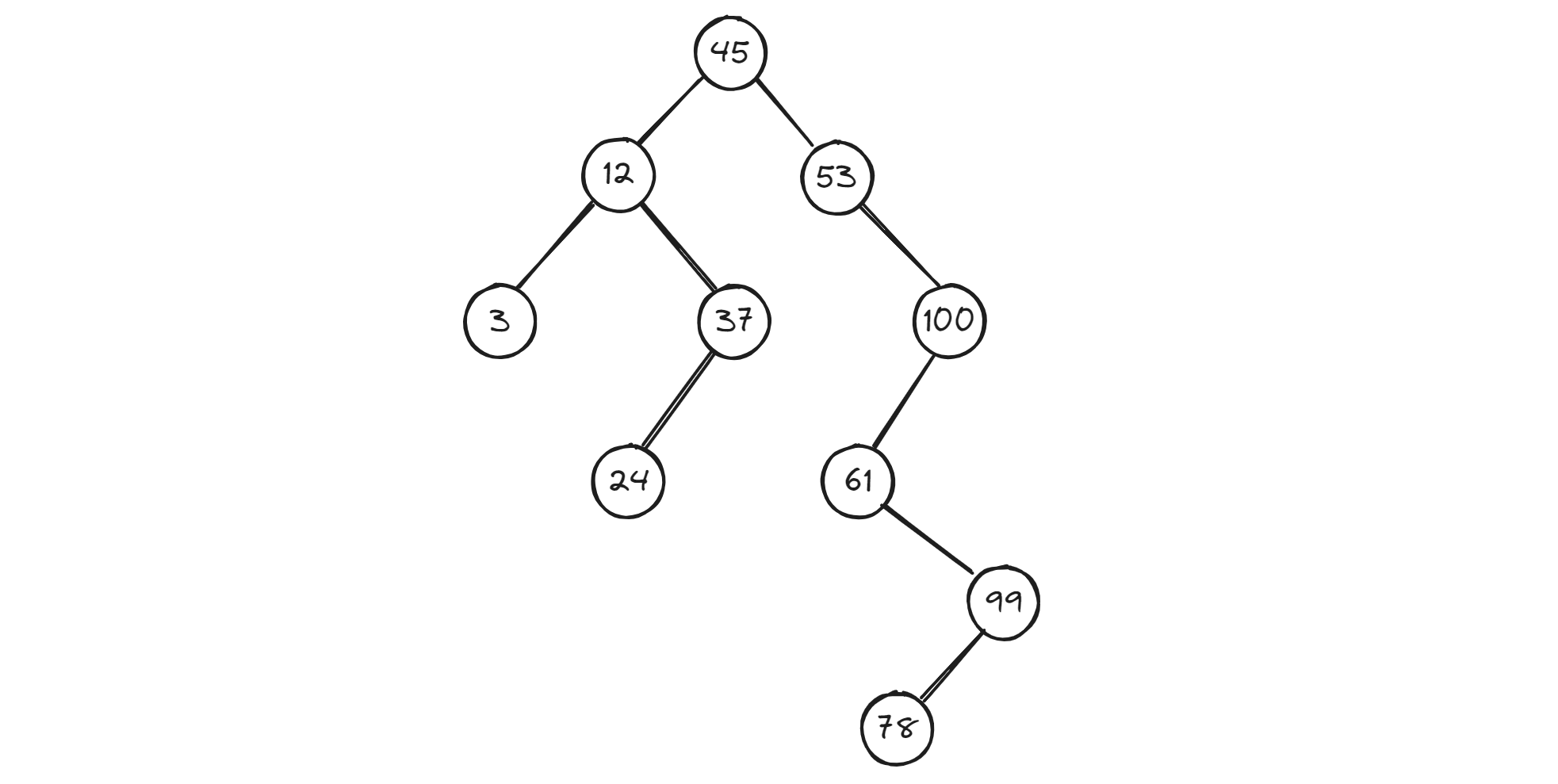
从上述的两个查找例子（key=100和key=40）可见，在二叉排序树上查找其关键字等于给定值的过程，恰是走了一条从根结点到该结点的路径的过程，和给定值比较的关键字个数等于路径长度加1（或结点所在层次数）。因此，和折半查找类似，与给定值比较的关键字个数不超过树的深度。然而，折半查找长度为n的顺序表时，其判定树是唯一的，而含有n个结点的二叉排序树却不唯一。例如，下图中的两棵二叉排序树。

image-20240213142948486

在这两棵二叉排序树中，结点的值都相同，但创建这两棵树的序列不同，分别是：(45, 24, 53, 12, 37, 93)和(12, 24, 37, 45, 53, 93)。图（a）所示树的深度为3，而图（b）所示树的深度为6。从平均查找长度来看，假设6个记录的查找概率相等，为1/6，则图（a）所示树的平均查找长度为：

ASL=16[1+2+2+3+3+3]=14/6ASL=\frac{1}{6}[1+2+2+3+3+3]=14/6

而图（b）所示树的平均查找长度为：

ASL=16[1+2+3+4+5+6]=21/6ASL=\frac{1}{6}[1+2+3+4+5+6]=21/6

因此，含有n个结点的二叉排序树的平均查找长度和树的形态有关。当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树。树的深度为n，其平均查找长度为n+12\frac{n+1}{2}（和顺序查找相同），这是最差的情况。显然，最好的情况是，二叉排序树的形态和折半查找的判定树相似，其平均查找长度为log⁡2n\log_{2}{n}。

若考虑把n个结点按各种可能的次序插入到二叉排序树中，则有n!n!棵二叉排序树（其中有的形态相同）。可以证明，综合所有可能的情况，就平均而言，二叉排序树的平均查找度仍然和log⁡2n\log_{2}{n}是同数量级的。

综上，二叉排序树的查找和折半查找相差不大。但就维护表的有序性而言，二叉排序树更加有效，因为无需移动记录，只需修改指针即可完成对结点的插入和删除操作。因此，对于需要经常进行插入、删除和查找运算的表，采用二叉排序树比较好。

三、插入

二叉排序树的插入操作是以查找为基础的。要将一个关键字值为key的结点*S插入到二叉排序树中，则需要从根结点向下查找，当树中不存在关键字等于key的结点时才进行插入。新插入的结点一定是一个新添加的叶子结点，并且是查找不成功时查找路径上访问的最后一个结点的左孩子或右孩子结点。其算法步骤为：

  • 若二叉排序树为空，则待插入结点*S作为根结点插入到空树中。
  • 若二叉排序树非空，则将key与根结点的关键字T->data.key进行比较：
    • 若key小于T->data.key，则在根结点的左子树中插入*s；
    • 若key大于T->data.key，则在根结点的右子树中插入*s。

相应的算法描述为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 当二叉排序树T中不存在关键字等于e.key的数据元素时，则插入该元素
void InsertBST(BSTree &T, ElemType e) {
    // 找到插入为止，递归结束
    if(!T) {
        // 生成新结点
        S=new BSTNode;
        // 新结点*S的数据域置为e
        S->data=e;
        // 新结点*S作为叶子结点
        s->lchild=S->rchild=NULL;
        // 将新结点*S链接到已找到的插入位置
        T=S;
    }
    else if(e.key<T->data.key)
        // 将*S插入左子树
        InsertBST(T->lchild,e);
    else if(e.key>T->data.key)
        // 将*S插入右子树
        InsertBST(T->rchild,e);
}

接下来，我们以下图为例，说明在二叉排序树中进行插入结点的过程：

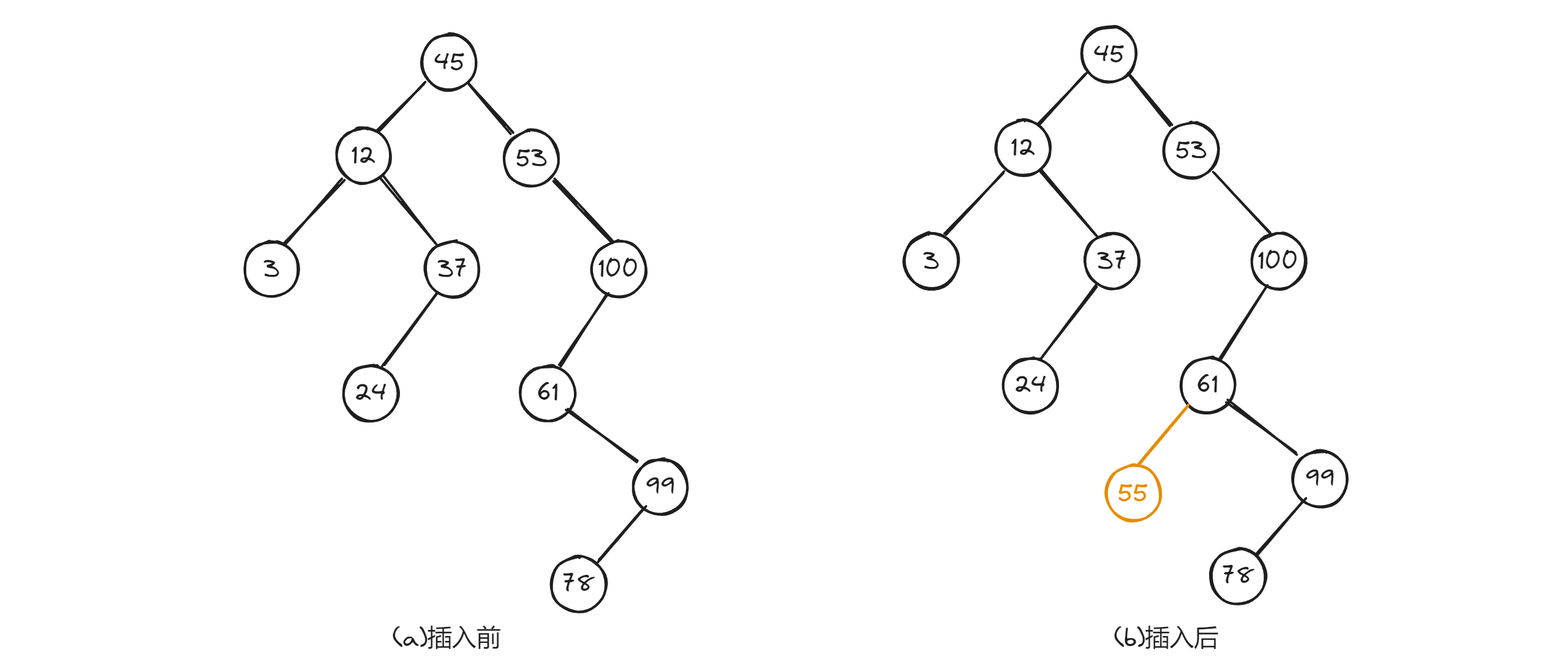
image-20240213144823624

在这棵二叉排序树中插入关键字为55的结点。由于插入前二叉排序树非空，故将55和根结点45进行比较，因55>45，则应将55插入到45的右子树上；然后，将55和45的右子树的根53比较，因55>53，则应将55插入到53的右子树上；依次类推，直至最后55<61，且61的左子树为空，所以将55作为61的左孩子插入到树中。

二叉排序树的插入操作，其基本过程是查找，所以时间复杂度同查找一样，是O(log⁡2n)O(\log_{2}{n})。

四、创建

二叉排序树的创建是从一棵空二叉排序树开始，每输入一个结点，经过查找操作，将新结点插入到当前二叉排序树的合适位置。其算法步骤为：

  • 将二叉排序树T初始化为空树。
  • 读入一个关键字为key的结点。
  • 如果读入的关键字key不是输入结束标志，则循环执行以下操作：
    • 将此结点插入二叉排序树T中；
    • 读入一个关键字为key的结点。

相应的算法描述为：

1
2
3
4
5
6
7
8
9
10
11
12
13
// 依次读入一个关键字为key的结点，将此结点插入到二叉排序树T中
void CreateBST(BSTree &T) {
    // 将二叉排序树T初始化为空树
    T=NULL;
    cin>>e;

    // ENDFLAG是输入结束标志，它是一个自定义常量
    while(e.key!=ENDFLAG) {
        // 将此结点插入到二叉排序树T中
        InsertBST(T,e);
        cin>>e;
    }
}

假设关键字的输入次序为：45, 24, 53, 45, 12, 24, 90，按上述算法二叉排序树的生成过程如下图所示。

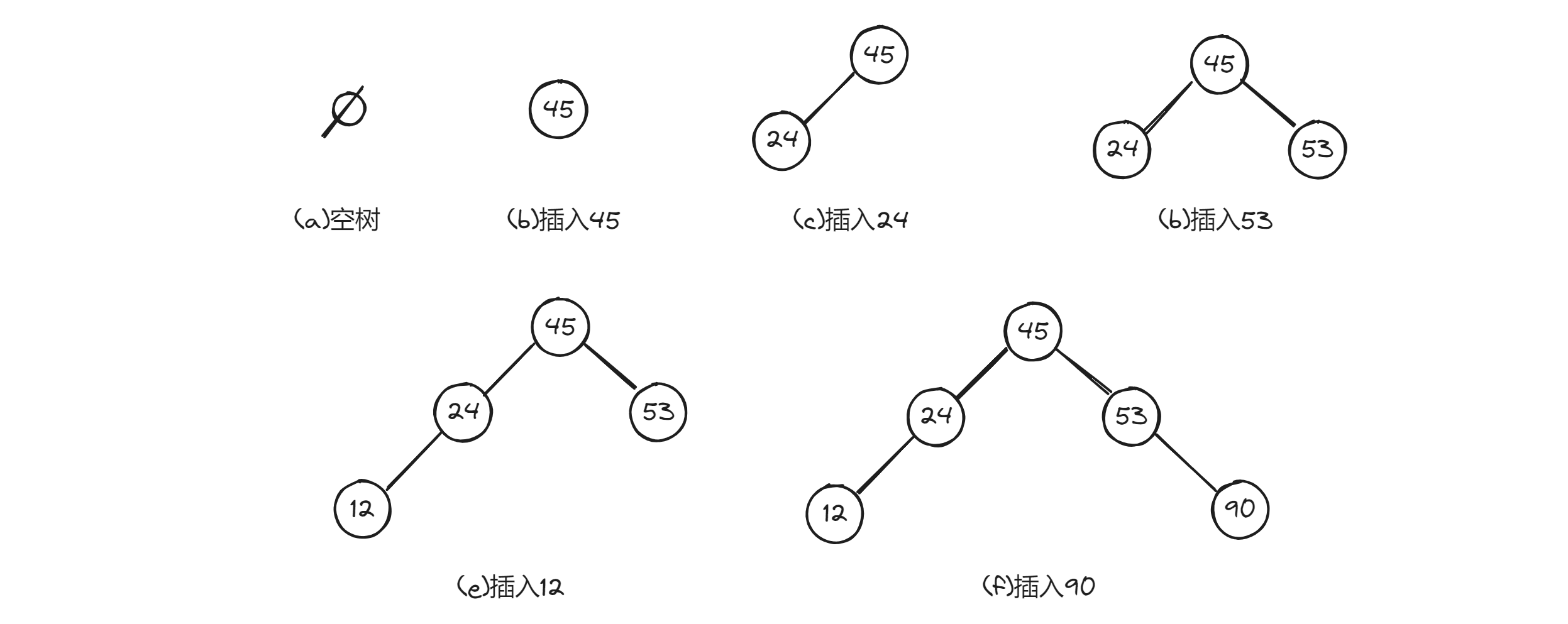
image-20240213150940731

可以看出，一个无序序列可以通过构造一棵二叉排序树而变成一个有序序列，构造树的过程就是对无序序列进行排序的过程。不仅如此，从上面的插入过程还可以看到，每次插入的新结点都是二叉排序树上新的叶子结点，则在进行插入操作时，不必移动其他结点，仅需改动某个结点的指针，由空变为非空即可。这就相当于在一个有序序列上插入一个记录而不需要移动其他记录。

当有n个结点时，需要进行n次插入操作，而插入一个结点的算法时间复杂度为O(log⁡2n)O(\log_2n)，所以创建二叉排序树算法的时间复杂度为O(nlog⁡2n)O(n\log_2n)。

五、删除

在二叉排序树中，被删除结点可能是树中的任意结点。因此，要根据被删除结点的位置，修改其双亲结点及相关结点的指针，以保持二叉排序树的特性。

5.1、删除过程

在二叉排序树中，删除某个节点，首先是从根结点开始，查找该结点，如果树中不存在此结点，则不做任何操作；否则，就要根据待删结点的位置，进行相应的处理。接下来，我们以下图为例，分析删除过程。

image-20240414095859438

在这里，我们假设被删结点为*p（指向该结点的指针为p），其双亲结点为*f（指向该结点的指针为f），PLP_L和PRP_R分别表示其左子树和右子树。不失一般性，可设*p是*f的左孩子（右孩子情况类似）。具体可分3种情况进行讨论。

结点*p为叶子结点，即PLP_L和PRP_R均为空树。

由于，删掉叶子结点，不破坏整棵树的结构。因此，只需修改其双亲结点的指针：

1
f->lchild=NULL;

结点*p只有左子树PLP_L或者只有右子树PRP_R。

此时，只需将PLP_L或PRP_R，修改为其双亲结点*f的左子树。

1
2
3
f->lchild=p->lchild;
or
f->lchild=p->rchild;

结点*p的左子树和右子树均非空。

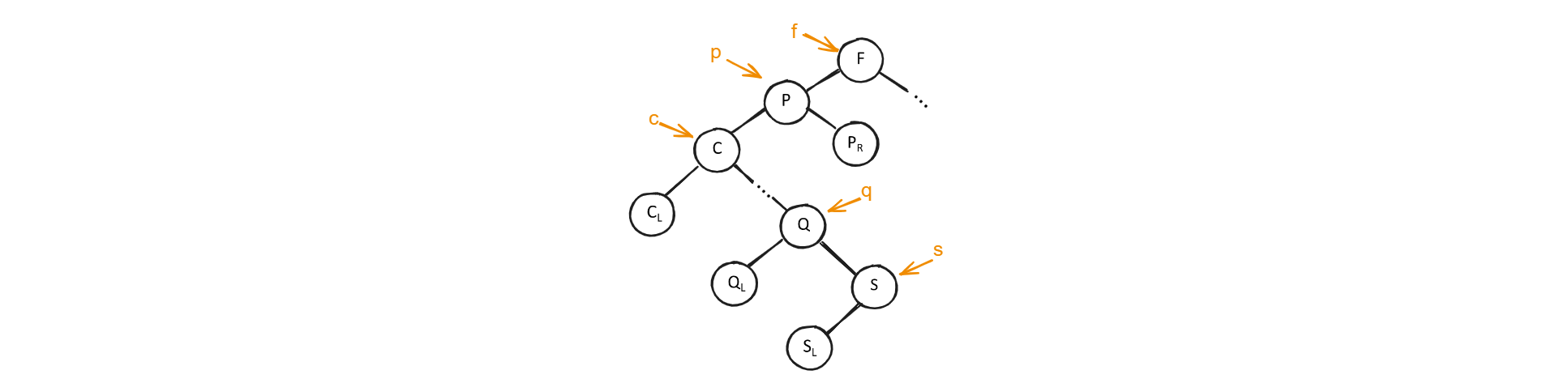
image-20240414094324038

从上图可知，在删去结点*p之前，中序遍历该二叉树得到的序列为(CL,C,...,QL,Q,SL,S,P,PR,F,...)(C_L,C,...,Q_L,Q,S_L,S,P,P_R,F,...)。在删去*p之后，为保持其他元素之间的相对位置不变，可以有两种处理方法：

  • 将*p的左子树，修改为*f的左子树，而*p的右子树为*s的右子树。如下图所示，

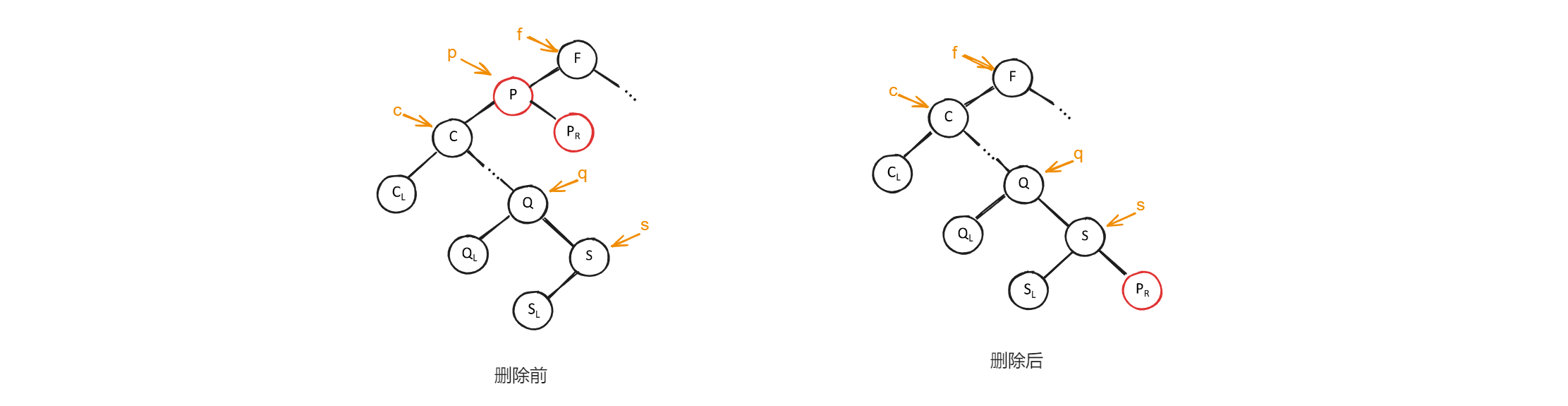
image-20240414100041461

1
2
f->lchild=p->lchild;
s->rchild=p->rchild;
  • 用*p的直接前驱（或直接后继）替代*p，并从二叉排序树中删掉它的直接前驱（或直接后继）。如下图所示，*p的直接前驱是*s。当用直接前驱*s替代*p时，由于*s只有左子树SLS_L，则在删掉*s之后，只要令SLS_L为*s的双亲*q的右子树即可。

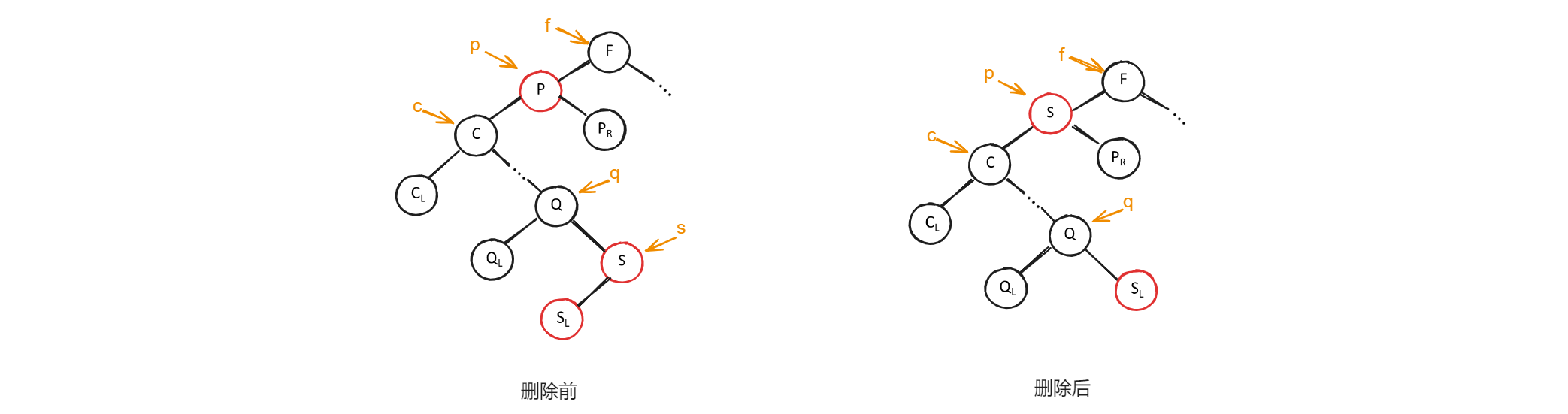
image-20240414100218538

1
2
p->data=s->data;
q->rchild=s->lchild;

显然，前一种处理方法可能增加树的深度，而后一种方法是用被删结点左子树中关键字最大的结点替代被删结点，并从左子树中删除这个结点。此结点一定没有右子树（否则它就不是左子树中关键字最大的结点），这样不会增加树的高度，所以在删除操作中，常采用这种处理方案（后面的算法描述使用该方案）。

5.2、算法描述

理解上述删除过程，就能给出相应的算法描述了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
// 从二叉排序树T中删除关键字等于key的结点
void DeleteBST(BSTree &T, KeyType key) {
    // 初始化
    f=NULL;
    p=T;

    // 从根开始查找关键字等于key的结点*p
    while(p) {
        // 找到关键字等于key的结点*p，结束循环
        if(key==p->data.key) break;

        // *f为*p的双亲结点
        f=p;
        // 在*p的左子树中继续查找
        if(key<p->data.key) p=p->lchild;
        // 在*p的右子树中继续查找
        else p=p->rchild;
    }
    // p为NULL，说明没有找到被删结点，直接返回
    if(!p) return;

    /*---- 考虑3种情况实现p所指子树内部的处理：*p左右子树均非空、无右子树、无左子树 -----*/
    // 被删结点*p左右子树均非空
    if( (p->lchild)&&(p->rchild) ) {
        q=p;
        s=p->lchild;

        // 在*p的左子树中查找其前驱结点（即最右下结点）
        while(s->rchild) {
            q=s;
            s=s->rchild;
        }

        // 以*s替代*p
        p->data=s->data;
        // 重接*q的右子树
        if(q!=p) q->rchild=s->lchild;
        // 重接*q的左子树
        else q->lchild=s->lchild;
        delete s;

        return;
    }
    // 被删结点*p右子树为空，只需重接其左子树
    else if(!p->rchild) {
        q=p;
        p=p->lchild;
    }
    // 被删结点*p左子树为空，只需重接其右子树
    else if(!p->lchild) {
        q=p;
        p=p->rchild;
    }

    /*---- 将p所指的子树挂接到其双亲结点*f相应的位置 ----*/
    // f为NULL，说明被删结点为根结点
    if(!f) T=p;
    // 将p所指的子树挂接到*f的左子树位置
    else if(q==f->lchild) f->rchild=p;
    // 将p所指的子树挂接到*f的右子树位置
    else f->rchild=p;

    delete q;
}

和插入一样，二叉排序树的删除过程也是查找，所以时间复杂度仍是O(log2n)O(log_2n)。

六、小结

二叉排序树（Binary Sort Tree），又称二叉查找树，是一种对排序和查找都很有用的特殊二叉树。在二叉排序树中，可以进行快速的查找、插入和删除操作。二叉排序树的平均时间复杂度为O(log2n)O(log_{2}{n})，但在最坏情况下可能退化为单支树，时间复杂度为O(n)O(n)。

img

七、参考

《数据结构（C语言版 第2版）》

《数据结构 自考02331》

数据结构
#数据结构
数据结构：树表的查找之二叉树排序
https://kuberxy.github.io/2024/03/31/数据结构18：树表的查找之二叉排序树/
作者
Mr.x
发布于
2024年3月31日
许可协议