数据结构：树表的查找之平衡二叉树

二叉排序树的性能取决于二叉排序树的结构，而二叉排序树的结构则取决于其数据集。如果数据集呈有序排序，则二叉排序树是线性的，查找的时间复杂度为 $O(n)$ ；反之，如果二叉排序树的结构合理，则查找速度较快，查找的时间复杂度为 $O(log_2n)$ 。简单来说就是，树的高度越小，查找速度越快。因此，我们希望二叉排序树的高度尽可能小，而平衡二叉树就能实现这一点。

一、定义

平衡二叉树（Balanced Binary Tree或Height-Balanced Tree），是一种特殊的二叉排序树。它由前苏联数学家阿德尔森-维尔斯基（Adelson-Velskii）和兰迪斯（Landis）提出，所以又称AVL树。

一棵平衡二叉树或者是空树，或者是具有如下特征的二叉排序树：

左子树和右子树的深度之差的绝对值不超过1；
左子树和右子树也是平衡二叉树。

如果将二叉树中结点的平衡因子（Balance Factor，BF）定义为该结点左子树和右子树的深度之差，则平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。例如，下图（a）是两棵平衡二叉树，下图（b）是两棵不平衡的二叉树。

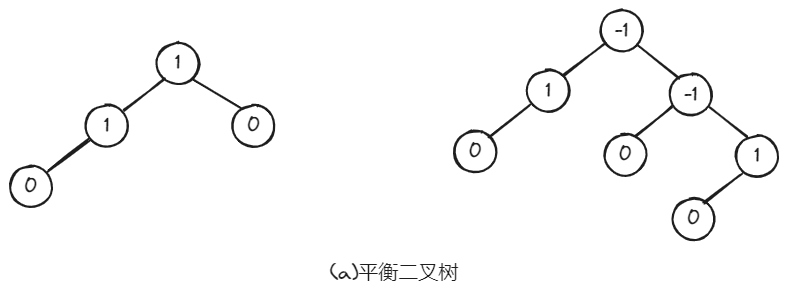
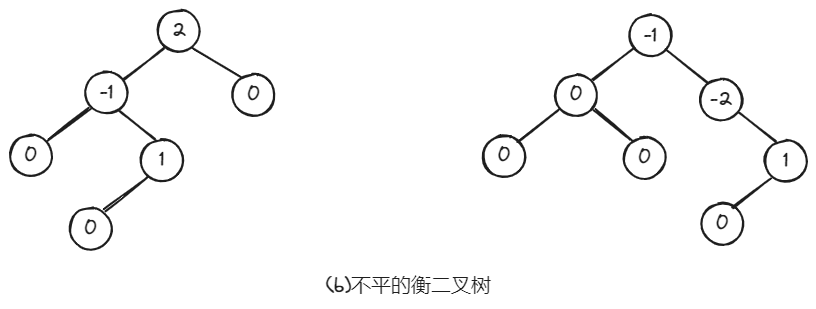
在平衡二叉树中，任何结点的左右子树的深度之差都不超过1，即它的高度和 $O(log_{2}{n})$ 是同数量级的（其中n为结点个数）。因此，平衡二叉树的查找性能不会出现退化现象，其查找的时间复杂度是 $O(log_{2}{n})$ 。

二、平衡调整方法

该如何创建一棵平衡二叉树呢？

插入结点时，按照二叉排序树的逻辑进行处理，若插入结点后破坏了平衡二叉树的特性，就需要对平衡二叉树进行调整。调整方法是：找到离插入结点最近且平衡因子绝对值超过1的祖先结点，以该结点为根的子树称为最小不平衡子树，可将重新平衡的范围局限于这棵子树。

我们先看一个具体的例子。假设表中关键字序列为 $(12,24,37,90,53)$ 。空树和只有1个结点13的树显然都是平衡的二叉树。在插入24之后二叉树仍是平衡的，只是树根结点的平衡因子由0变为−1。

在继续插入37之后，由于结点13的平衡因子由−1变成−2，出现了不平衡的现象。这就好比一根扁担出现一头重、一头轻的现象，若能将扁担的支撑点由13改至24，扁担的两头就平衡了。由此，可以对树做一个“左逆时针旋转”操作，令结点24为根，结点13成为它的左子树。此时，结点13和结点24的平衡因子都为0，而且仍保持二叉排序树的特性。

在相继插入结点90、结点53之后，结点24和节点37的平衡因子都由−1变成了−2，出现了新的不平衡现象。此时，因为是结点53插在结点90的左子树上，所以不能做之前的简单调整。在这种情况下，离插入结点最近的最小不平衡子树是以结点37为根的子树。必须以结点53作为根结点，结点37成为它的左子树的根，结点90成为它的右子树的根。这好比对树做了两次“旋转”操作，先向右顺时针旋转，后向左逆时针旋转，使二叉排序树由不平衡转化为平衡。

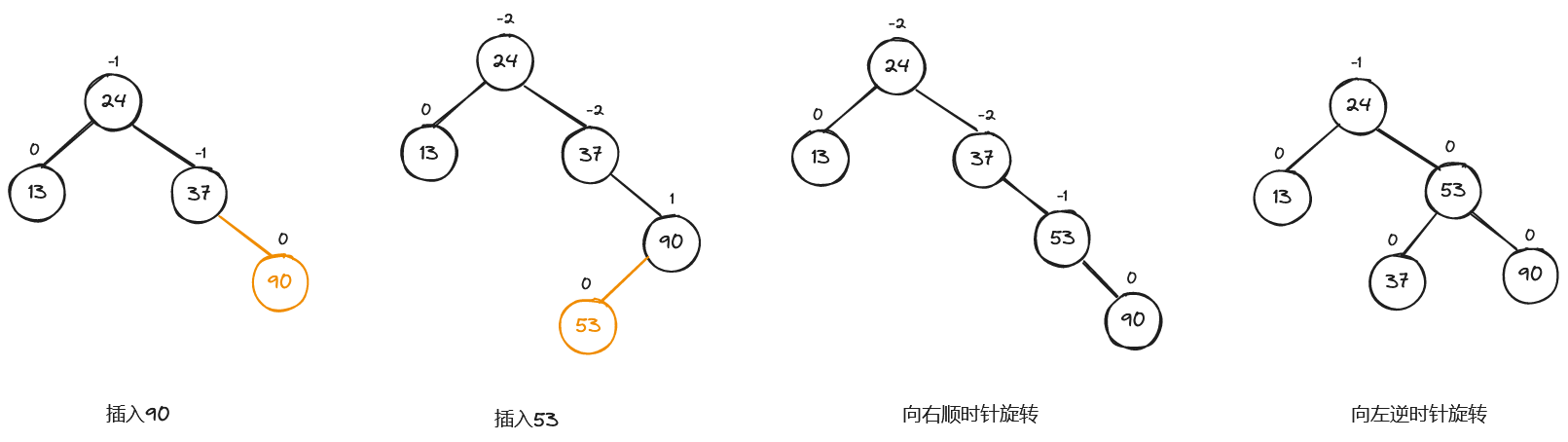
接下来，我们讨论一般情况，假设最小不平衡子树的根结点为A，则失去平衡后进行调整的规律可归纳为4种情况。

2.1、LL型

如下图，在A的左子树根结点的左子树上插入结点，A的平衡因子由1增至2，致使以A为根结点的子树失去平衡，需进行一次向右的顺时针旋转操作。

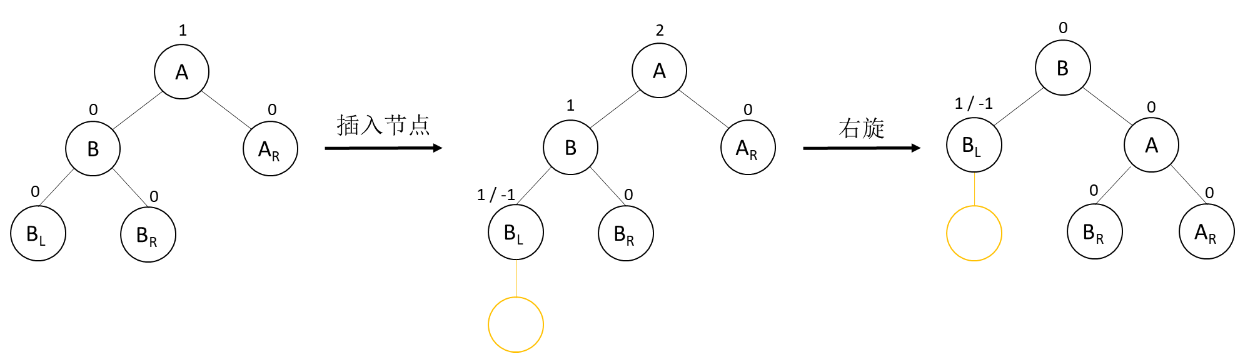
如下，是LL型的两种具体调整示例。

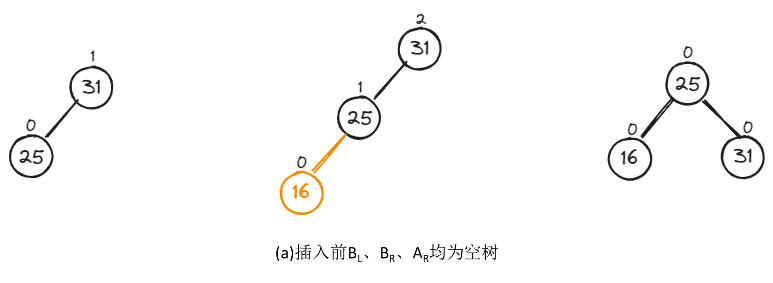
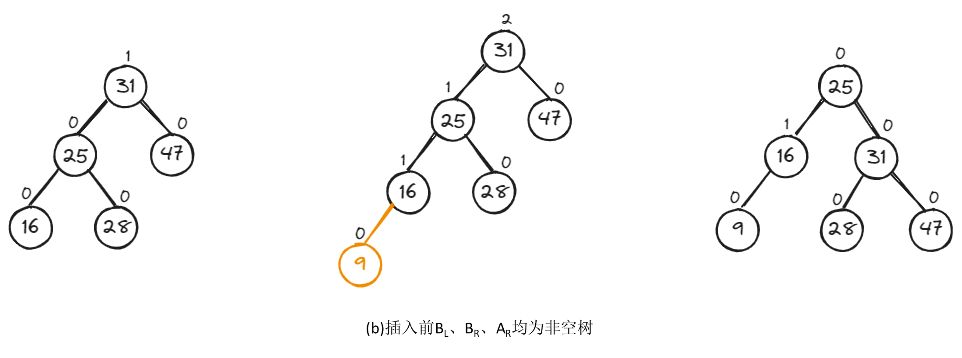
2.2、RR型

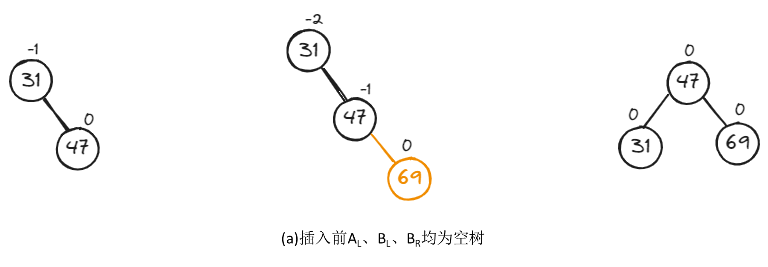
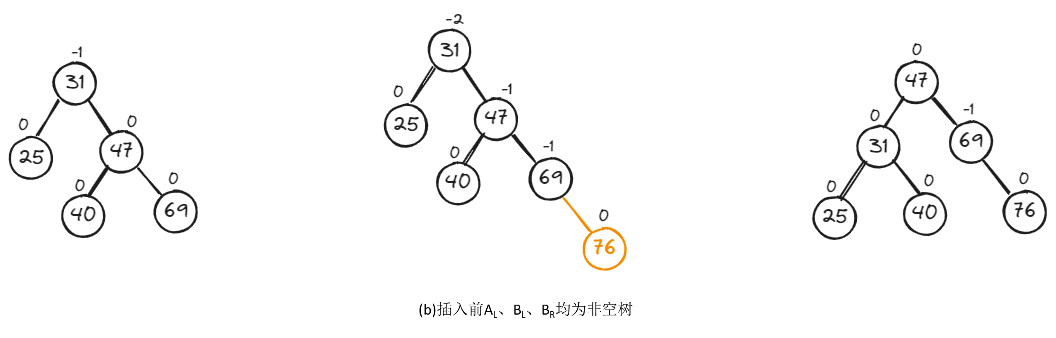
如下图，在A的右子树根结点的右子树上插入结点，A的平衡因子由-1增至-2，致使以A为根结点的子树失去平衡，需进行一次向左的逆时针旋转操作。

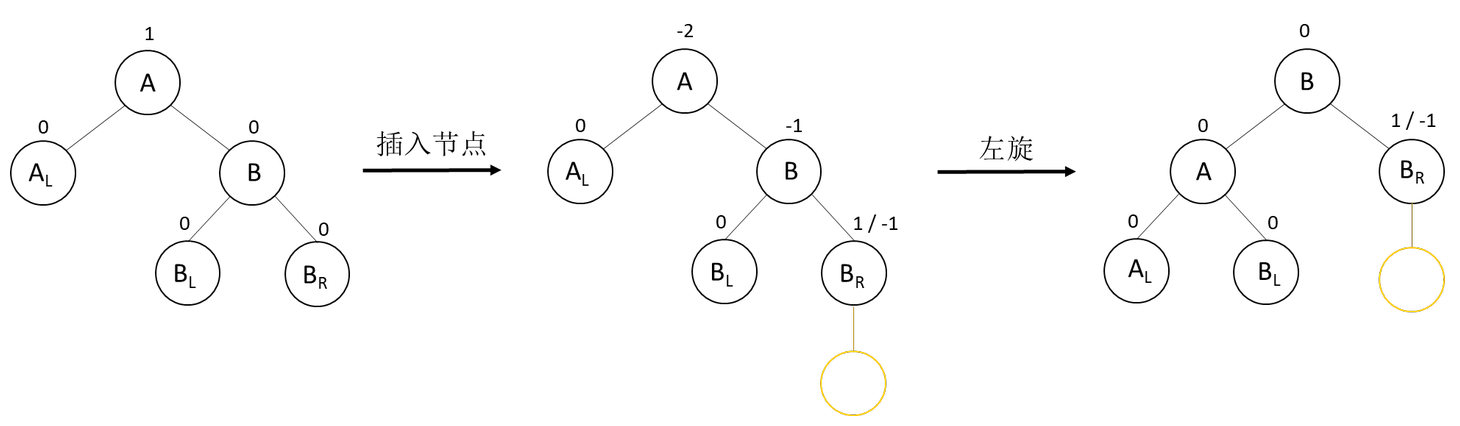
如下，是RR型的两种具体调整示例。

2.3、LR型

如下图，在A的左子树根节点的右子树上插入结点，A的平衡因子由1增至2，致使以A为根结点的子树失去平衡，需进行两次旋转操作。第一次向左对B及其右子树进行逆时针旋转，C转上去成为B的根，这时变成了LL型，所以第二次进行LL型的向右顺时针旋转即可恢复平衡。如果C原来有左子树，则调整C的左子树为B的右子树。

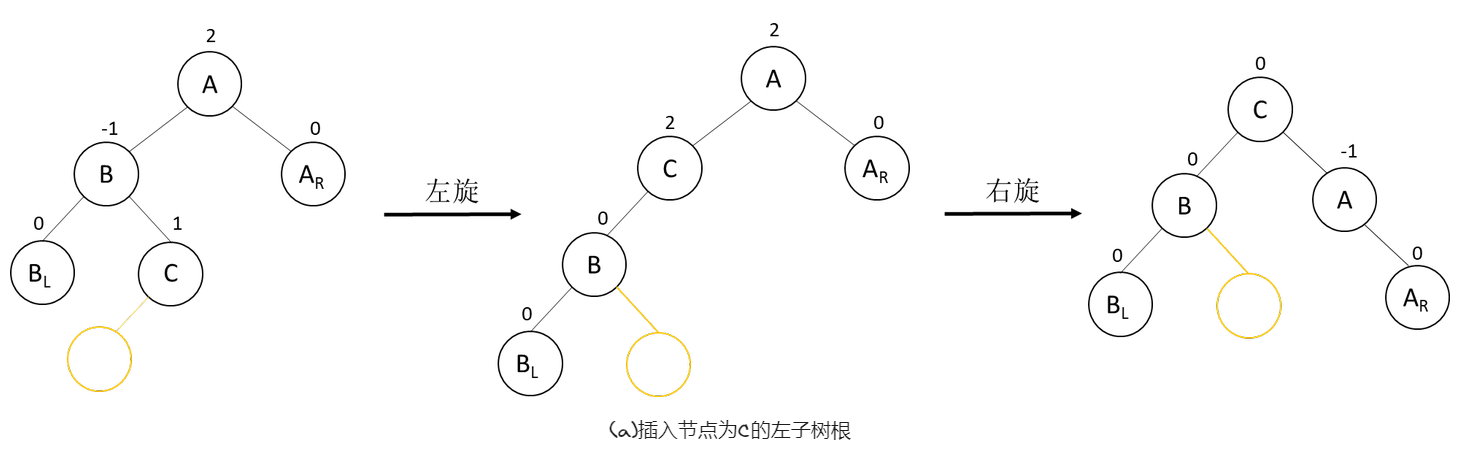
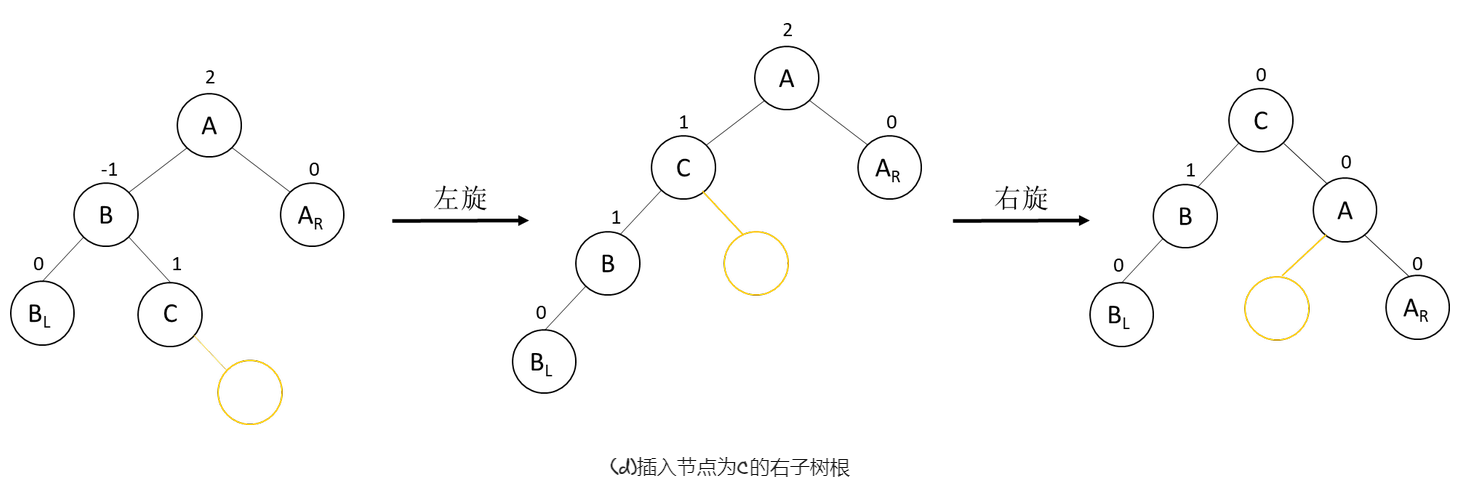
如下，是LR型的三种具体调整示例。

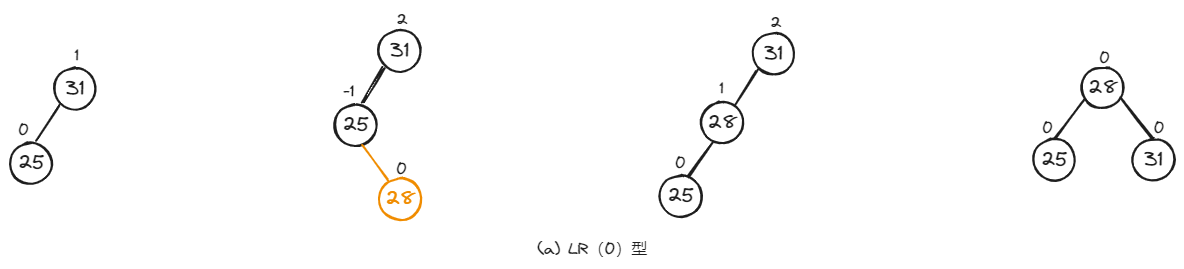
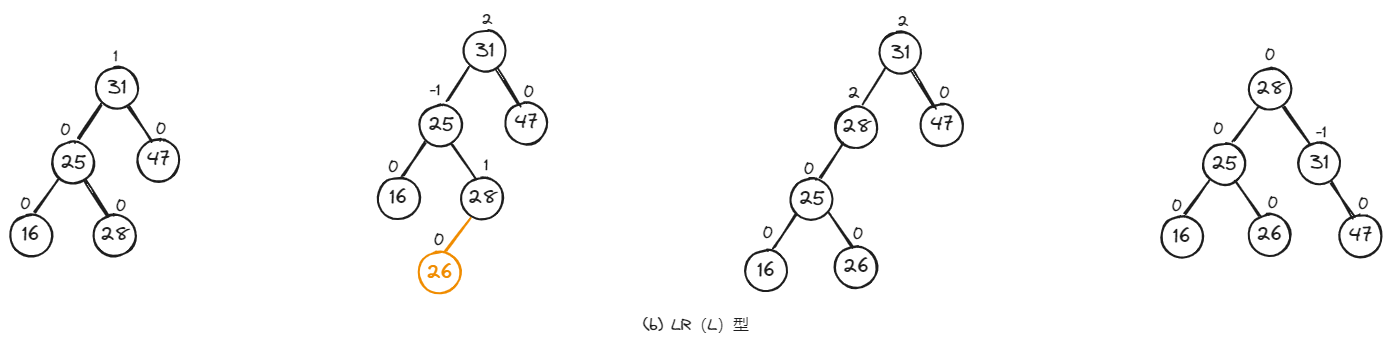
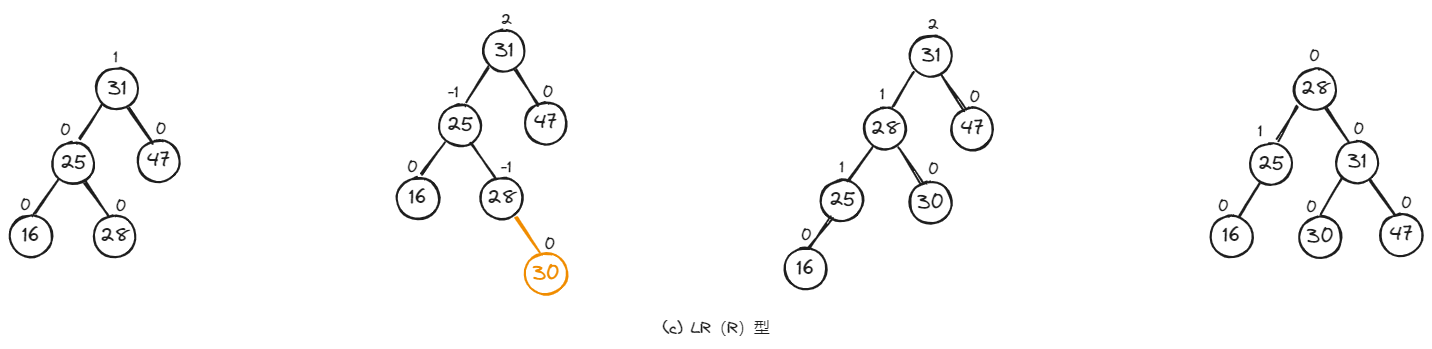
2.4、RL型

如下图，在A的右子树根结点的左子树上插入结点，A的平衡因子由-1变成-2，致使以A为根结点的子树失去平衡，需进行两次旋转。第一次向右顺时针旋转，第二次向左逆时针旋转。

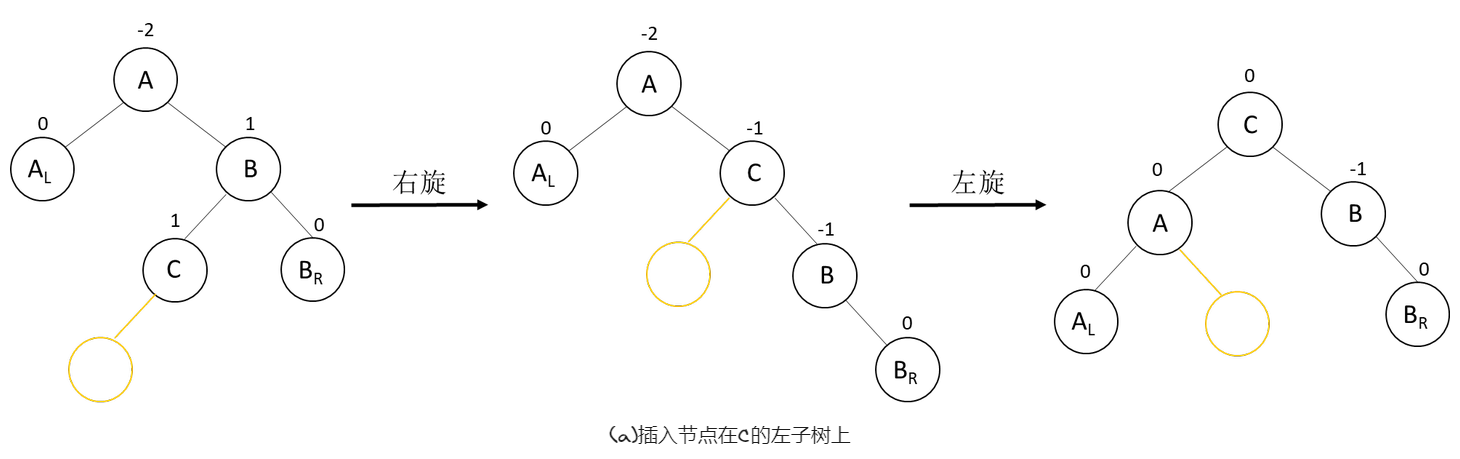
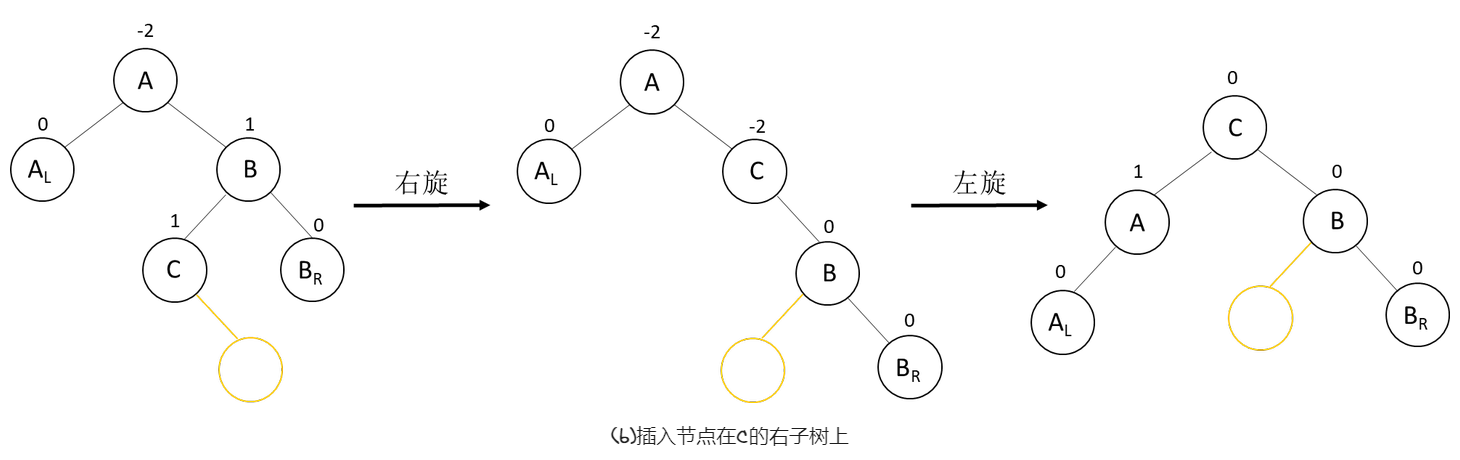
如下，是RL型的三种具体调整示例。

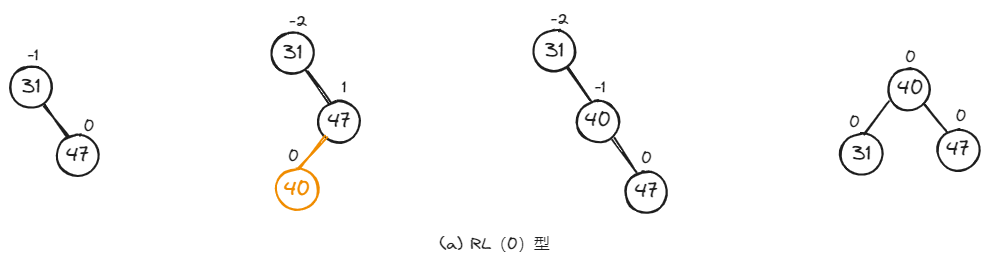
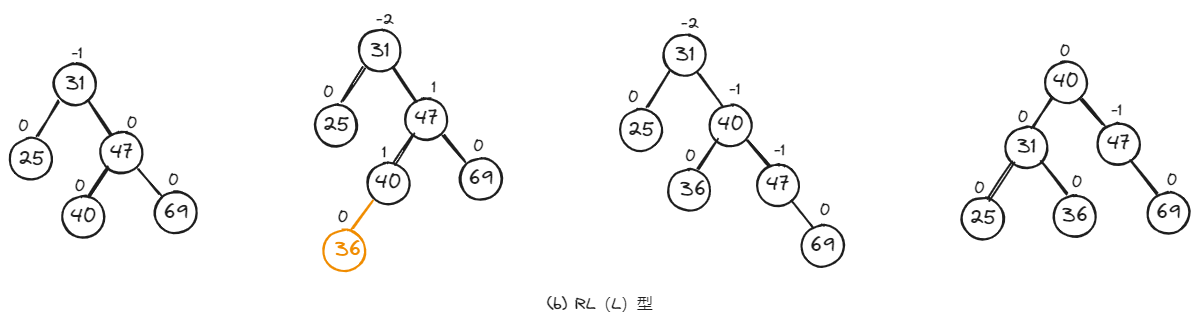
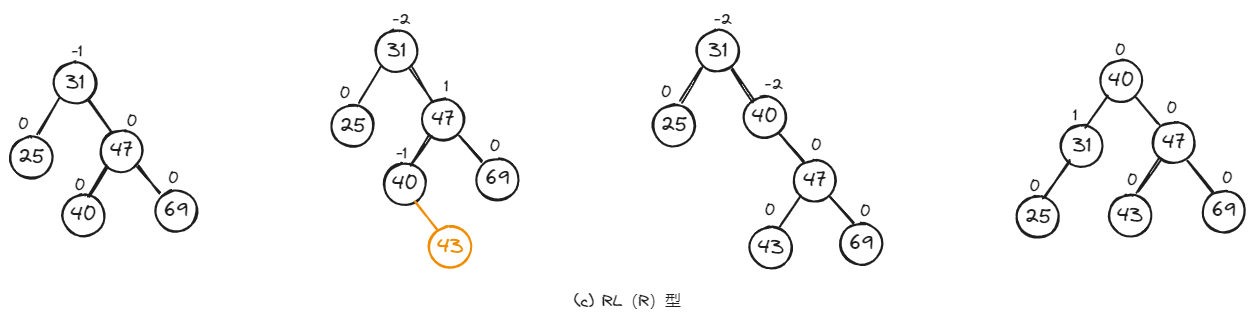
2.5、小结

上述4种情况中，LL型和RR型对称，LR型和RL型对称。旋转操作的正确性可由“保持二叉排序树的特性：中序遍历所得关键字序列自小至大有序“证明。

此外，无论哪一种情况，在经过平衡调整之后，以B或C为根的新子树为平衡二叉树，而且它们的深度和插入之前以A为根的子树相同。因此，当平衡的二叉排序树因插入结点而失去平衡时，仅需对最小不平衡子树进行平衡旋转处理即可。因为经过旋转处理之后的子树深度和插入之前相同，因而不影响插入路径上所有祖先结点的平衡度。

三、插入

在平衡二叉树BBT上插入一个新的数据元素e的算法步骤如下：

若BBT为空树，则插入一个数据元素为e的新结点作为BBT的根结点，树的深度增1。
若e的关键字和BBT的根结点的关键字相等，则不进行插入。
若e的关键字小于BBT的根结点的关键字，且在BBT的左子树中不存在和e有相同关键字的结点，则将e插入到BBT的左子树上。插入之后左子树深度增1，分别就下列不同情况进行处理：
- BBT的根结点的平衡因子为-1（右子树的深度大于左子树的深度）：将根结点的平衡因子更改为0，BBT的深度不变；
- BBT的根结点的平衡因子为0（左、右子树的深度相等）：将根结点的平衡因子更改为1，BBT的深度增1；
- BBT的根结点的平衡因子为1（左子树的深度大于右子树的深度）：
  - 若BBT的左子树根结点的平衡因子为1，则需进行单向右旋平衡处理，并且在旋转处理之后，将根结点和其右子树根结点的平衡因子更改为0，树的深度不变；
  - 若BBT的左子树根结点的平衡因子为-1，则需进行先左后右的两次旋转平衡处理，并且在旋转处理之后，修改根结点和其左、右子树根结点的平衡因子，树的深度不变。
若e的关键字大于BBT的根结点的关键字，且在BBT的右子树中不存在和e有相同关键字的结点，则将e插入到BBT的右子树上。插入之后右子树深度增1，分别就下列不同情况进行处理：
- BBT的根结点的平衡因子为1（左子树的深度大于右子树的深度）：将根结点的平衡因子更改为0，BBT的深度不变；
- BBT的根结点的平衡因子为0（左、右子树的深度相等）：将根结点的平衡因子更改为-1，BBT的深度增1；
- BBT的根结点的平衡因子为-1（右子树的深度大于左子树的深度）：
  - 若BBT的左子树根结点的平衡因子为-1，则需进行单向左旋平衡处理，并且在旋转处理之后，将根结点和其左子树根结点的平衡因子更改为0，树的深度不变；
  - 若BBT的左子树根结点的平衡因子为1，则需进行先右后左的两次旋转平衡处理，并且在旋转处理之后，修改根结点和其左、右子树根结点的平衡因子，树的深度不变。