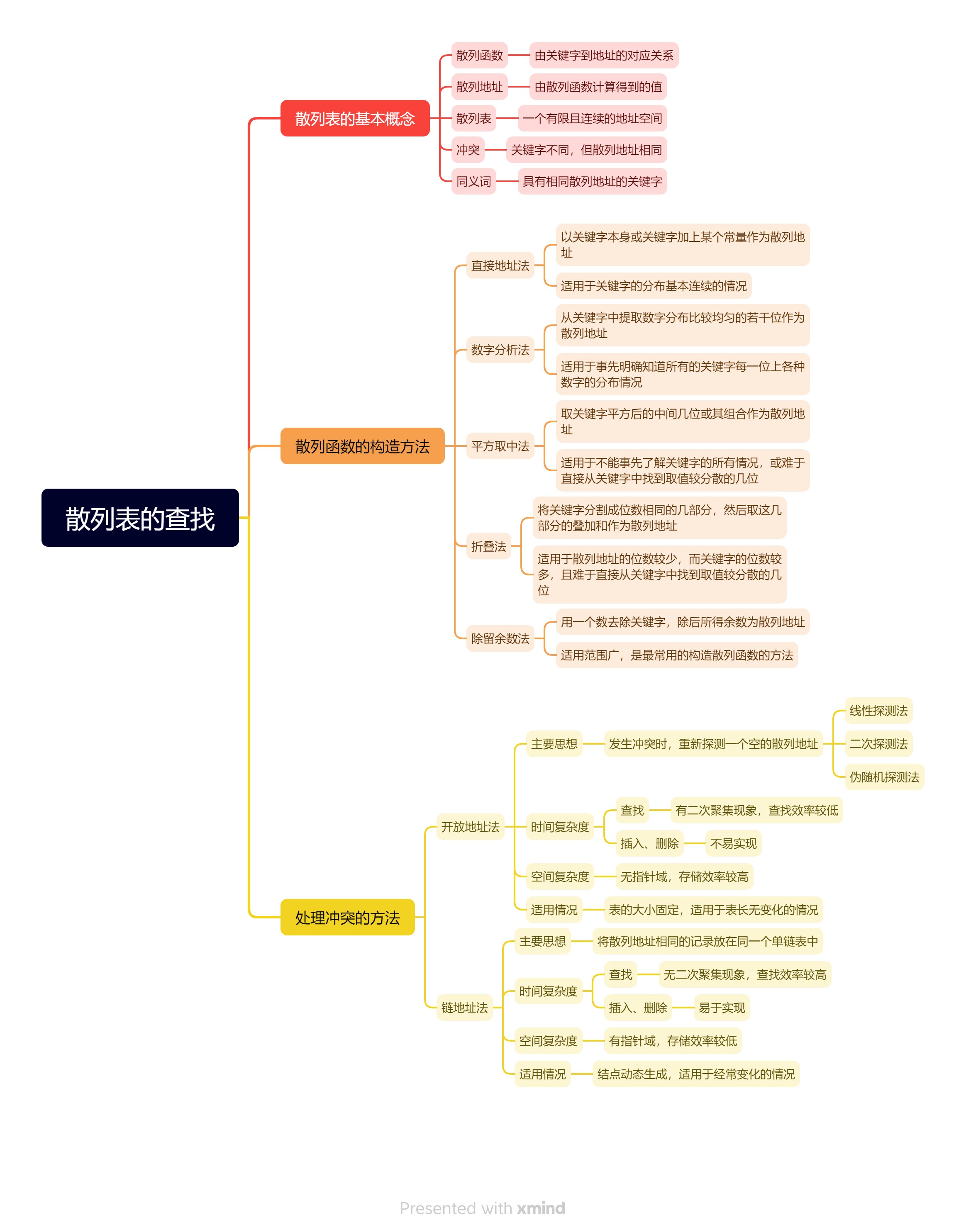
数据结构：散列表的查找

线性表和树表的查找方法都是以关键字的比较为基础。查找过程中只考虑各元素关键字之间的相对大小，元素在存储结构中的位置和其关键字无直接关系，查找时间与表的长度有关。当表中结点个数很多时，查找时要大量地与无效结点的关键字进行比较，致使查找速度很慢。

如果能在元素的存储位置和其关键字之间建立某种直接关系，直接由关键字找到相应的元素，那么在进行查找时，就无需进行比较或仅需做很少次的比较，查找效率能大幅提升。而这正是散列查找法（Hash Search）的思想。

一、散列表的基本概念

散列查找法（又称哈希查找法、杂凑法或散列法），是一种由关键字到地址的直接查找方法。 它通过对元素的关键字值进行某种运算，直接求出元素的存储地址。在散列查找法中，常用的术语如下。

  • 散列函数和散列地址：在元素的存储位置p和其关键字key之间建立一种确定的对应关系H，使得p=H(key)，则称这个对应关系H为散列函数，p为散列地址。
  • 散列表：一个有限且连续的地址空间，用以存储由散列函数计算得出的散列地址的数据记录。通常，散列表的存储空间是一个一维数组，散列地址是数组的下标。
  • 冲突和同义词：对于不同的关键字可能得出相同的散列地址，即key1≠key2key_1 \neq key_2，而H(key1)=H(key2)H(key_1)=H(key_2)，这种现象称为冲突。具有相同散列地址的关键字，对该散列函数来说称作同义词，即当key1≠key2key_1 \neq key_2，而H(key1)=H(key2)H(key_1)=H(key_2)时，key1key_1与key2key_2互称为同义词。

例如，对C语言中的某些关键字集合建立一个散列表。现假设关键字集合为

S1={main,int,float,while,return,break,switch,case,do}S_1=\{main, int, float, while, return, break, switch, case, do\}

对于该集合，设定一个长度为26的散列表应该足够，散列表可定义为：

1
char HT[26][8];

假设散列函数的值取为关键字key中第一个字母在字母表{a, b,…, z}中的序号（序号范围为0～25），即

H(key)=key[0]−′a′H(key)=key[0]-'a'

其中，设key的类型是长度为8的字符数组。根据此散列函数构造的散列表如下表所示。

0 1 2 3 4 5 … 8 … 12 … 17 18 … 22 … 25
break case do flat int main return switch while

假设关键字集合扩充为：

S2=S1+{short,default,double,static,for,struct}S_2=S_1+\{short, default, double, static, for, struct\}

如果散列函数不变，新加入的7个关键字经过计算得到：H(short)=H(static)=H(struct)=18H(short)=H(static)=H(struct)=18，H(default)=H(double)=3H(default)=H(double)=3，H(for)=5H(for)=5，而18、3和5这几个位置均已存放相应的关键字，这就发生了冲突现象，其中，switch、short、static和struct称为同义词；do、default和double称为同义词；float和for称为同义词。

集合S2S_2中的关键字仅有15个，仔细分析这15个关键字的特性，应该不难构造一个散列函数避免冲突。但在实际应用中，理想化的、不产生冲突的散列函数极少存在，这是因为关键字的取值集合远远大于表空间的地址集。例如，高级语言的编译程序要对源程序中的标识符建立一张符号表进行管理，多数都采取散列表。在设定散列函数时，要考虑的关键字集合应包含所有可能产生的关键字，不同的源程序中使用的标识符一般也不相同，如果此语言规定标识符为长度不超过8的、字母开头的字母数字串，字母区分大小写，则标识符取值集合的大小为：

C521×C627×7!=1.09×1012\mathrm{C}_{52}^{1} \times \mathrm{C}_{62}^{7} \times 7!=1.09 \times 10^{12}

而一个源程序中出现的标识符是有限的，所以编译程序将散列表的长度设为1000足矣。于是，要将多达101210^{12}个可能的标识符映射到有限的地址上，难免产生冲突。通常，散列函数是一个多对一的映射，所以冲突是不可避免的，只能通过选择一个“好”的散列函数使得在一定程度上减少冲突。而一旦发生冲突，就必须采取相应措施及时予以解决。

综上所述，散列查找法主要研究以下两方面的问题：

  • 如何构造散列函数；
  • 如何处理冲突；

二、散列函数的构造方法

构造散列函数的方法很多，一般来说，应根据具体问题选用不同的散列函数。在构造散列函数时，通常要考虑以下因素：

  • 散列表的长度；
  • 关键字的长度；
  • 关键字的分布情况；
  • 计算散列函数所需的时间；
  • 记录的查找频率

构造一个“好”的散列函数应遵循以下两条原则：

  • 函数计算要简单，每一关键字只能有一个散列地址与之对应；
  • 函数的值域需在散列表的长度范围内，计算出的散列地址的分布应均匀，尽可能减少冲突。

下面介绍几种构造散列函数的常用方法。

2.1、直接地址法

直接地址法，是以关键字本身或关键字加上某个常量C作为散列地址的方法。对应的散列函数为：

H(key)=key+CH(key)=key+C

在使用时，为了使散列地址与存储空间吻合，可以调整C。这种方法计算简单，并且没有冲突。适合于关键字的分布基本连续的情况，若关键字分布不连续，空号较多，将会造成较大的空间浪费。

2.2、数字分析法

数字分析法，是假设有一组关键字，每个关键字由n位数组成，如k1k2...knk_1k_2...k_n。且每个关键字的位数比散列表的地址码位数多，则可以从关键字中提取数字分布比较均匀的若干位作为散列地址。

例如，有80个记录，其关键字为8位十进制数。假设散列表的表长为100，则可取两位十进制数组成散列地址，选取的原则是分析这80个关键字，使得到的散列地址尽量避免产生冲突。假设这80个关键字中的一部分如下所列：

关键字 散列地址（00…99）
81346532 46
81372242 72
81387422 87
81301367 01
81322817 22
81338967 38
81354157 64
81368537 68
81419355 19

对关键字全体的分析中可以发现：第1、2位都是81，第3位只可能取3或4，第8位可能取2、5或7，因此这4位都不可取。由于中间的4位可看成是近乎随机的，因此可取其中任意两位，或取其中两位与另外两位的叠加求和后舍去进位作为散列地址。

数字分析法适用于：事先明确知道所有的关键字每一位上各种数字的分布情况。例如，同一出版社出版的所有图书，其ISBN号的前几位都是相同的，因此，若数据表只包含同一出版社的图书，构造散列函数时可以利用这种数字，只分析排除ISBN号前几位后的数字。

2.3、平方取中法

平方取中法，是一种较常用的构造散列函数的方法。它是取关键字平方后的中间几位或其组合作为散列地址。因为在多数情况下，不一定能知道关键字的全部情况，直接取其中几位也不一定合适，而一个数平方后的中间几位数和数的每一位都相关，故由此产生的散列地址较为均匀。

例如，为源程序中的标识符建立一个散列表，假设标识符为字母开头的由字母和数字组成的串。假设人为约定每个标识的内部编码规则如下：把字母在字母表中的位置序号作为该字母的内部编码，如I的内部编码为09，D的内部编码为04，A的内部编码为01。数字直接用其自身作为内部编码，如1的内部编码为01，2的内部编码为02。根据以上编码规则，可知“IDA1”的内部编码为09040101，同理可以得到“IDB2”、“XID3”和“YID4”的内部编码。之后分别对内部编码进行平方运算，再取出第7位到第9位作为其相应标识符的散列地址，如下表所示。

标识符 内部编码 内部编码的平方 散列地址
IDA1 09040101 081723426090201 426
IDB2 09040202 081725252200804 252
XID3 24090403 580347516702409 516
YID4 25090404 629528372883216 372

平方取中法适用于：不能事先了解关键字的所有情况，或难于直接从关键字中找到取值较分散的几位。

2.4、折叠法

折叠法，是指将关键字分割成位数相同的几部分（最后一段的位数可以少一些），然后取这几部分的叠加和（舍去进位）作为散列地址。

根据数位叠加的方式，可以把折叠法分为移位叠加和边界叠加。移位叠加是将分割后每一部分的最低位对齐，然后相加；边界叠加是将两个相邻的部分沿边界来回折叠，然后对齐相加。

例如，当散列表长为1000时，关键字key=45387765213，从左到右按3位数一段分割，可以得到4个部分：453、877、652、13。分别采用移位叠加和边界叠加，求得散列地址为995和914，如下图所示。

img

折叠法适用于：散列地址的位数较少，而关键字的位数较多，且难于直接从关键字中找到取值较分散的几位。

2.5、除留余数法

假设散列表的表长为m，选择一个不大于m的数p，用p去除关键字，除后所得余数为散列地址，即

H(key)=key%pH(key)=key \% p

该方法的关键是选取适当的p，一般情况下，可以选p为小于表长的最大质数。例如，表长m=100，可取p=97。

除留余数法计算简单，适用范围非常广，是最常用的构造散列函数的方法。它不仅可以对关键字直接取模，也可在折叠、平方取中等运算之后取模，这样能够保证散列地址一定落在散列表的地址空间中。

三、处理冲突的方法

选择一个“好”的散列函数可以在一定程度上减少冲突，但在实际应用中，很难完全避免发生冲突，所以选择一个有效的处理冲突的方法是散列法的另一个关键问题。创建散列表和查找散列表都会遇到冲突，两种情况下处理冲突的方法应该一致。下面以创建散列表为例，来说明处理冲突的方法。

处理冲突的方法与散列表本身的组织形式有关。按组织形式的不同，通常分两大类：开放地址法和链地址法。

3.1、开放地址法

开放地址法的基本思想是：当某一记录关键字key的初始散列地址H0=H(key)H_0=H(key)发生冲突时，以H0H_0为基础，采取合适的方法计算得出另一个地址H1H_1 ，如果H1H_1仍然发生冲突，以H1H_1为基础再求下一个地址H2H_2，若H2H_2仍然冲突，再求得H3H_3 。依次类推，直至HkH_k不发生冲突为止，则HkH_k为该记录在表中的散列地址。

该方法在寻找“下一个”空的散列地址时，数组空间对所有的元素都是开放的，所以称为开放地址法。通常，我们把寻找“下一个”空位的过程称为探测。开放地址法可用如下公式表示：

Hi=(H(key)+di)%mi=1,2,...,k(k≤m−1)H_i=(H(key)+d_i)\%m \qquad i=1,2,...,k(k \le m-1)

其中，H(key)为散列函数，m为散列表的表长，did_i为增量序列。根据did_i取值的不同，可以分为以下3种探测方法。

（1）线性探测法

di=1,2,3,⋅⋅⋅,m−1d_i=1,2,3,···,m-1

这种探测方法可以将散列表假想成一个循环表，发生冲突时，从冲突地址的下一单元顺序寻找空单元，如果到最后一个位置也没找到空单元，则回到表头开始继续查找，直到找到一个空位，就把此元素放入此空位中。如果找不到空位，则说明散列表已满，需要进行溢出处理。

（2）二次探测法

d1=12,−12,22,−22,⋅⋅⋅,k2,−k2(k≤m/2)d_1=1^2,-1^2,2^2,-2^2,···,k^2,-k^2(k \le m/2)

（3）伪随机探测法

di=伪随机数序列d_i=伪随机数序列

例如，散列表的长度为11，散列函数H(key)=key%11H(key)=key\%11，假设表中已填有关键字分别为17、60、29的记录，如下图所示。

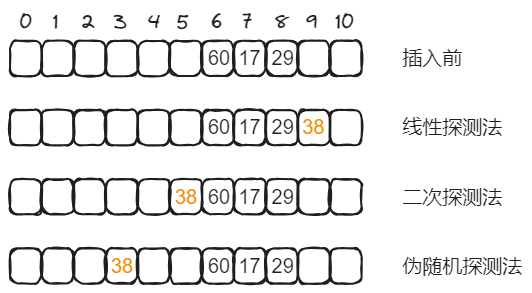
image-20240512162139295

现有第四个记录，其关键字为38，由散列函数得到散列地址为5，产生冲突。

  • 若用线性探测法处理时，得到下一个地址6，仍冲突；再求下一个地址7，仍冲突；直到散列地址为8的位置为“空”时为止，处理冲突的过程结束，38填入散列表中序号为8的位置。
  • 若用二次探测法，散列地址5冲突后，得到下一个地址6，仍冲突；再求得下一个地址4，无冲突，38填入序号为4的位置。
  • 若用伪随机探测法，假设产生的伪随机数为9，则计算下一个散列地址为(5+9)%11=3，所以38填入序号为3的位置。

从线性探测法的处理过程，可以看到一个现象：当表中位置i 、i+1、i+2上已填有记录时，散列地址为i 、i+1、i+2和i+3的记录都将填入i+3的位置。这种在处理冲突过程中发生的两个第一个散列地址不同的记录争夺同一个后继散列地址的现象称作“二次聚集 ”（或称作“堆积 ”），即在处理同义词的冲突过程中又添加了非同义词的冲突。

可以看出，上述三种处理方法各有优缺点。线性探测法的优点是：只要散列表未填满，总能找到一个不发生冲突的地址。缺点是：会产生“二次聚集”现象。而二次探测法和伪随机探测法的优点是：可以避免“二次聚集”现象。缺点也很显然：不能保证一定找到不发生冲突的地址。

3.2、链地址法

链地址法的基本思想是：把具有相同散列地址的记录放在同一个单链表（又称同义词链表）中。有m个散列地址就有m个单链表，同时用数组HT[0…m−1]存放各个链表的头指针，凡是散列地址为i的记录，都以结点方式，插入到以HT[i]为头结点的单链表中。

例如，已知一组关键字为（19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79），设散列函数H(key)=key %13。用链地址法处理冲突，由散列函数H(key)=key %13可得出散列地址的值域为0～12，故整个散列表有13个单链表组成，用数组HT[0…12]存放各个链表的头指针。如散列地址均为1的同义词14、1、27、79构成一个单链表，链表的头指针保存在HT[1]中，同理，可以构造其他几个单链表，整个散列表的结构如下图所示。

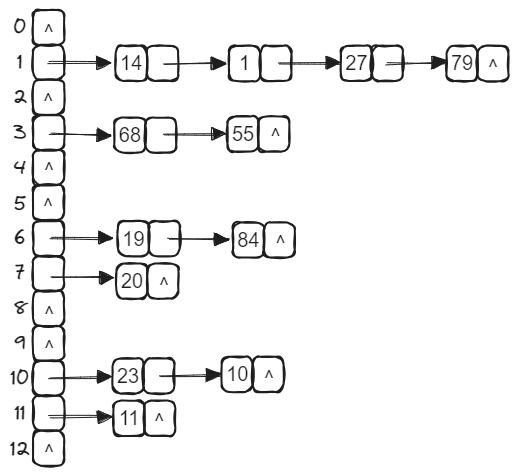
image-20240512165456634

这种构造方法在具体实现时，依次计算各个关键字的散列地址，然后根据散列地址将关键字插入到相应的链表中。

四、散列表的查找

在散列表上进行查找的过程和创建散列表的过程基本一致。下面，以开放地址法（线性探测法）处理冲突为例，给出在散列表中进行查找的过程。开放地址法散列表的存储表示如下：

1
2
3
4
5
6
7
8
9
// 散列表的表长
#define m 20

typedef struct {
    // 关键字项
    KeyType key;
    // 其他数据项
    InfoType otherinfo;
}HashTable[m];

4.1、算法步骤

在散列表中进行查找的算法步骤为：

  • 给定待查找的关键字key，根据建表时设定的散列函数计算H0=H(key)H_0=H(key)；
  • 若单元H0H_0为空，则所查元素不存在；
  • 若单元H0H_0中元素的关键字为key，则查找成功；
  • 否则重复下述解决冲突的过程：
    • 按处理冲突的方法，计算下一个散列地址HiH_i；
    • 若单元HiH_i为空，则所查元素不存在；
    • 若单元HiH_i中元素的关键字为key，则查找成功。

4.2、算法描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 单元为空的标记
#define NULLKEY 0

// 在散列表HT中查找关键字为key的元素，若查找成功，返回散列表的单元标号，否则返回-1
int SearchHash(HashTable HT, KeyType key) {
    // 根据散列函数H(key)计算散列地址
    H0=H(Key);
    // 若单元H0为空，则所查元素不存在
    if(HT[H0].key==NULLKEY) return -1;
    // 若单元H0中元素的关键字为key，则查找成功
    else if(HT[H0].key==key) return H0;
    else {
        for(i=1;i<m;++i) {
            // 按照线性探测法计算下一个散列地址Hi
            Hi=(H0+i)%m;
            // 若单元Hi为空，则所查元素不存在
            if(HT[Hi].key==NULLKEY) return -1;
            // 若单元Hi中元素的关键字为key，则查找成功
            else if(HT[Hi].key==key) return Hi;
        }
        return -1;
    }
}

4.3、算法分析

从散列表的查找过程可见：

  • 虽然散列表在关键字与记录的存储位置之间建立了直接映射，但由于“冲突”的产生，使得散列表的查找过程仍然是一个给定值和关键字进行比较的过程。因此，仍需以平均查找长度作为衡量散列表查找效率的量度。

  • 查找过程中需和给定值进行比较的关键字的个数取决于三个因素：散列函数、处理冲突的方法和散列表的装填因子。

    散列表的装填因子α\alpha定义为：

    α=表中填入的记录数散列表的长度\alpha = \frac{表中填入的记录数}{散列表的长度}

    α\alpha表示散列表的装填程度。直观地看，α\alpha越小，发生冲突的可能性就越小；反之，α\alpha越大，表中已填入的记录越多，再填记录时，发生冲突的可能性就越大，则查找时，给定值需与之进行比较的关键字的个数也就越多。

  • 散列函数的“好坏”首先影响出现冲突的频繁程度。但一般情况下认为：凡是“均匀的”散列函数，对同一组随机的关键字，产生冲突的可能性相同。假如所设定的散列函数是“均匀”的，则影响平均查找长度的因素只有两个——处理冲突的方法和装填因子α\alpha。

    下表给出了在等概率情况下，采用几种不同方法处理冲突时，得到的散列表查找成功和查找失败时的平均查找长度。

img

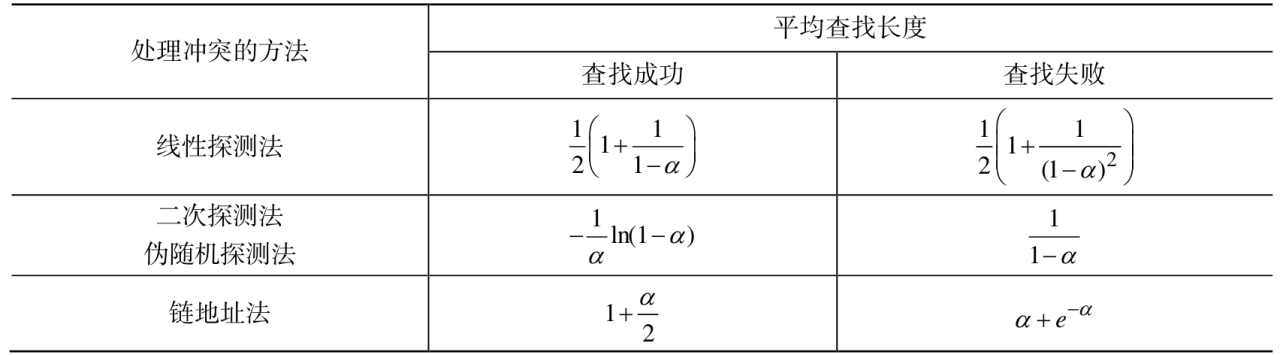
  • 从上表可以看出，散列表的平均查找长度是α\alpha的函数，而不是记录个数n的函数。由此，在设计散列表时，不管n多大，总可以选择合适的α\alpha以便将平均查找长度限定在一个范围内。

对于一个具体的散列表，通常可采用直接计算的方法求其平均查找长度，下面我们通过一个具体的示例来说明。

4.4、案例分析

关键字为(19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79)，散列函数为H(key)=key%13，用线性探测法处理冲突。设表长为16，试构造这组关键字的散列表，并计算查找成功和查找失败时的平均查找长度。

4.4.1、开放地址法

采用开放地址法，依次计算各个关键字的散列地址，如果没有冲突，将关键字直接存放在相应的散列地址所对应的单元中；否则，用线性探测法处理冲突，直到找到相应的存储单元中。

对于前三个关键字进行计算，H(19)=6，H(14)=1，H(23)10，所得散列地址均没有冲突，直接填入所在单元。而对于第四个关键字，H(1)=1，发生冲突，根据线性探测法，求得下一个地址(1+1)%16=2，没有冲突，所以1填入序号为2的单元。同理，可依次填入其他关键字。对于最后一个关键字79，H(79)=1，发生冲突，用线性探测法处理冲突，后面的地址2～8均有冲突，最终79填入9号单元。

最终构造结果如下表所示，表中最后一行的数字表示放置该关键字时所进行的关键字比较次数。

散列地址 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
关键字 14 1 68 27 55 19 20 84 79 23 11 10
比较次数 1 2 1 4 3 1 1 3 9 1 1 3

要查找一个关键字key，根据前面的查找算法可知，首先用散列函数计算H0=H(key)，然后进行比较，比较的次数和创建散列表时放置此关键字的比较次数是相同的。例如，查找关键字19时，计算散列函数H(19)=6，HT[6].key非空且值为19，查找成功，关键字比较次数为1次。同样，当查找关键字14、68、20、23、11时，均需比较1次即查找成功。当查找关键字1时，计算散列函数H(1)=1，HT[1].key非空且值为14≠1，用线性探测法处理冲突，计算下一个地址为(1+1)%16=2，HT[2].key非空且值为1，查找成功，关键字比较次数为2次。当查找关键字55，84，10时，需比较3次；当查找27时，需比较4次；而查找79时，需要比较9次才能查找成功。

在记录的查找概率相等的前提下，这组关键字采用线性探测法处理散列表冲突时，查找成功时的平均查找长度为

ASLok=112(1∗6+2+3∗3+4+9)=2ASL_{ok}=\frac{1}{12} (1 * 6 + 2 + 3 * 3 + 4 + 9)=2

查找失败时有两种情况：单元为空和按处理冲突的方法探测后仍未找到。

假设散列函数的取值个数为r，则0到r−1相当于r个查找失败的入口，从每个入口进入后，直到确定查找失败为止，其关键字的比较次数就是与该入口对应的查找失败的查找长度。比如，在该例中，散列函数的取值个数为13，即总共有13个查找失败的入口（0到12），对每个入口依次进行计算。

假设待查找的关键字不在表中。若H(key)=0，HT[0].key为空，则比较1次即确定查找失败。若H(key)=1，HT[1].key非空，则依次向后比较，直到HT[13].key为空，总共比较13次才能确定查找失败。类似地，对H(key)=2, 3,…, 12进行分析，可得查找失败的平均查找长度为

ASLerror=113(1+13+12+11+10+9+8+7+6+5+4+3+2)=7ASL_{error}=\frac{1}{13} (1+13+12+11+10+9+8+7+6+5+4+3+2)=7

4.4.2、链地址法

采用链地址法，依次计算各个关键字的散列地址，将散列地址相同的记录放在同一个单链表中，并将链表的头指针保存在数组HT中。

散列地址均为1的同义词14、1、27、79构成一个单链表，链表的头指针保存在HT[1]中，同理，可以构造其他几个单链表，最终构造结果如下图所示。

image-20240512165456634

每个单链表中的第1个结点的关键字（如14、68、19、20、23、11），查找成功时只需比较1次，第2个结点的关键字（如1、55、84、10），查找成功时需比较2次，第3个结点的关键字27需比较3次，第4个结点的关键字79则需比较4次才能查找成功。这时，查找成功时的平均查找长度为

ASLok=112(1∗6+2∗4+3+4)=1.75ASL_{ok}=\frac{1}{12} (1*6+2*4+3+4)=1.75

假设待查找的关键字不在表中。若H(key)=0，HT[0].key为空，则比较1次即确定查找失败。若H(key)=1，HT[1]所指的单链表包括4个结点，所以需要比较5次才能确定失败。类似地，对H(key)=2, 3,…, 12进行分析，可得查找失败的平均查找长度为

ASLerror=113(1+5+1+3+1+1+3+2+1+1+3+2+1+1+3+2+1)=1ASL_{error}=\frac{1}{13} (1+5+1+3+1+1+3+2+1+1+3+2+1+1+3+2+1)=1

4.4.3、小结

线性探测法在处理冲突的过程中易产生记录的二次聚集，散列地址不相同的记录会产生新的冲突；而用链地址法处理冲突则不会发生类似情况，因为散列地址不同的记录在不同的链表中，所以链地址法的平均查找长度小于开放地址法。另外，由于链地址法的结点空间是动态申请的，无需事先确定表的容量，因此更适用于表长不确定的情况。同时，易于实现插入和删除操作。

通过上面的示例，可以看出，在查找概率相等的前提下，直接计算查找成功的平均查找长度可以采用以下公式

ASLok=1n∑i=1nCiASL_{ok}=\frac{1}{n} \sum_{i=1}^{n} C_i

其中，n为散列表中记录的个数，CiC_i为成功查找第i个记录所需的比较次数。而直接计算查找失败的平均查找长度可以采用以下公式

ASLerror=1r∑i=1rCiASL_{error}=\frac{1}{r} \sum_{i=1}^{r} C_i

其中，r为散列函数取值的个数，CiC_i为散列函数取值为i时查找失败的比较次数。

五、总结

散列表也属线性结构，但它和线性表的查找有着本质的区别。它不是以关键字比较为基础进行查找的，而是通过一种散列函数把记录的关键字和它在表中的位置建立起对应关系，并在存储记录发生冲突时采用专门的处理冲突的方法。这种方式构造的散列表，不仅平均查找长度和记录总数无关，而且可以通过调节装填因子，把平均查找长度控制在所需的范围内。

散列查找法主要研究两方面的问题：如何构造散列函数，以及如何处理冲突。构造散列函数的方法很多，除留余数法是最常用的构造散列函数的方法。它不仅可以对关键字直接取模，也可在折叠、平方取中等运算之后取模。而处理冲突的方法则通常分为两大类：开放地址法和链地址法，二者之间的差别类似于顺序表和单链表的差别。其中，开放地址法的主要思想是，在发生冲突时，重新探测一个空的散列地址；而链地址法的主要思想是，将散列地址相同的记录放在同一个单链表中。

img

六、参考

《数据结构（C语言版 第2版）》

《数据结构 自考02331》

数据结构
#数据结构
数据结构：散列表的查找
https://kuberxy.github.io/2024/04/21/数据结构21：散列表的查找/
作者
Mr.x
发布于
2024年4月21日
许可协议