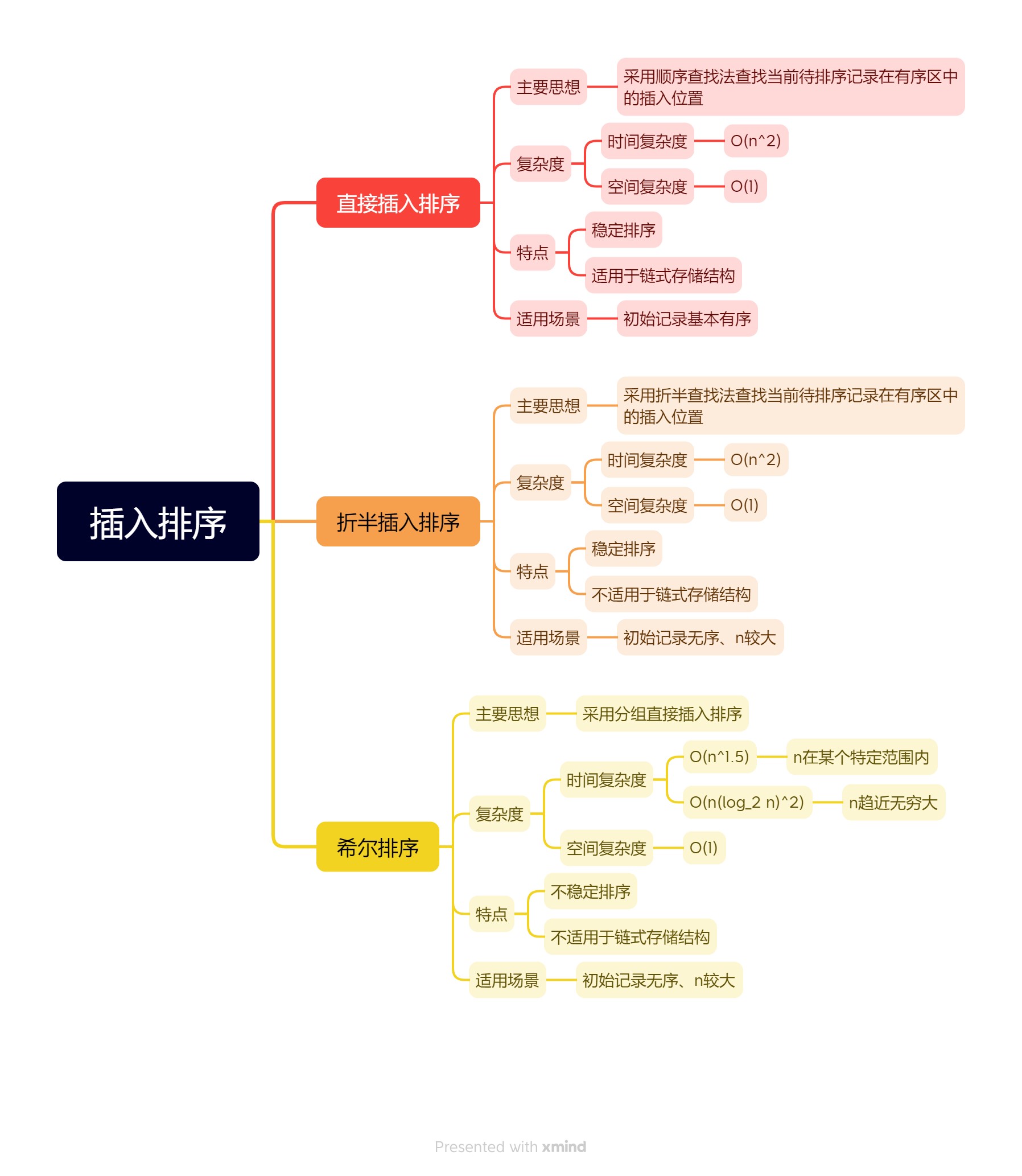
数据结构：插入排序

插入排序的基本思想是：每趟排序，将无序区中的一个记录，按排序要求插入到有序区的适当位置上，直到整个序列有序为止。例如，在打扑克牌时，如果要保证抓到的牌有序排列，则每抓一张牌，就插入到合适的位置，直到抓完牌为止，即可得到一个有序序列。

在有序区中寻找插入位置，可以选择不同的查找方法。根据查找方法的不同，有多种插入排序方法，本文将讨论常用的三种方法：直接插入排序、折半插入排序和希尔排序。

一、直接插入排序

直接插入排序（Straight Insertion Sort），采用顺序查找法，寻找待排序记录在有序区中的插入位置。

1.1、算法步骤

直接插入排序的算法步骤为：

设待排序记录存放在数组r[1…n]中，初始有序区为r[1]
循环n-1次，执行以下操作：
- 使用顺序查找法，在有序区r[1…i-1]中查找r[i]的插入位置
- 将r[i]插入到表长为i-1的有序区r[1…i-1]中

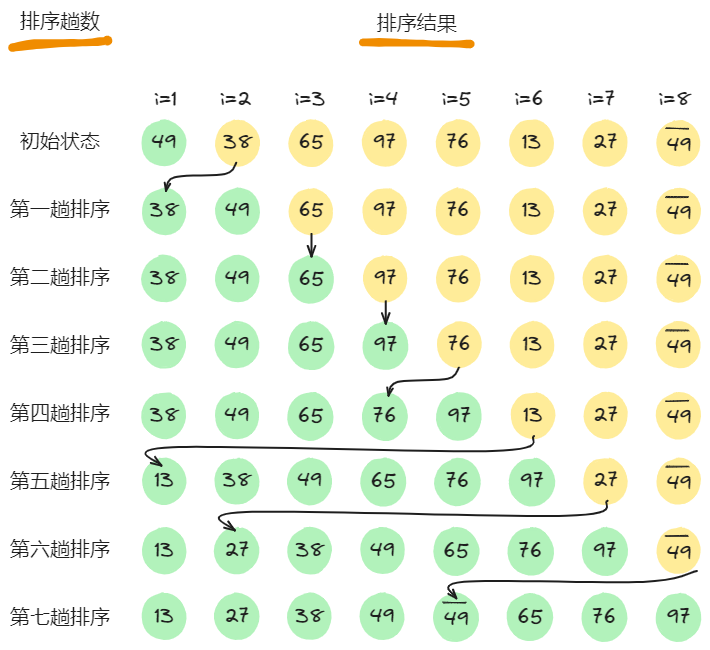
如下图，是对一组关键字序列为 $\{49,38,65,97,76,13,27, \overline{49}\}$ 的待排序记录，进行直接插入排序的过程，其中绿色为有序区，黄色为无序区。

1.2、算法描述

具体实现在有序区中查找r[i]的插入位置，有以下两种方法：

一种是将r[i]与r[1]，r[2]，···，r[i-1]从前向后顺序比较
一种是将r[i]与r[r-1]，r[r-2]，···，r[1]从后向前顺序比较

这里我们采用后一种方法。在自r[i-1]到r[1]从后向前查找插入位置的过程中，可以同时后移记录。

和顺序查找类似，在查找插入位置的过程中，为了避免数组下标出界，在r[0]处设置监视哨。相应的算法描述如下：

// 对顺序表L进行直接插入排序
void InsertSort(SqList &L) {
    // 长度为n的表，要进行n-1趟排序
    for(i=2;i<=L.length;++i) {
        // r[i]小于有序区中的最大值，需在有序区中查找r[i]的插入位置
        if(L.r[i].key<L.[i-1].key) {
            // 将待插入记录暂存到监视哨中
            L.r[0]=L.r[i];
            // 将r[i-1]后移到r[i]中
            r.r[i]=L.r[i-1];

            // 从后向前寻找插入位置,并后移记录
            for(j=i-2; L.r[0].key<L.r[j].key; --j) {
                // 记录逐个后移，直到找到插入位置
                L.r[j+1]=L.r[j];
            }

            // 将r[0]即原r[i]插入到正确位置
            L.r[j+1]=L.r[0];
        }
    }
}

1.3、算法分析

从时间上来看，排序的基本操作为：比较两个关键字的大小和移动记录。

对于任意一趟插入排序来说，上述算法中内层for循环的执行次数取决于待插记录的关键字与前i-1个记录的关键字之间的关系。其中，在最好情况（正序：待排序序列中记录按关键字非递减有序排列）下，比较1次，不移动；在最坏情况（逆序：待排序序列中记录按关键字非递增有序排列）下，比较i次（依次同前面的i−1个记录进行比较，并和哨兵比较1次），移动i+1次（前面的i−1个记录依次向后移动，另外开始时将待插入的记录移动到监视哨中，最后找到插入位置，又从监视哨中移过去）。

对于整个排序过程需执行n−1趟，最好情况下，总的比较次数为最小值n−1，记录不需移动；最坏情况下，总的关键字比较次数KCN和记录移动次数RMN均达到最大值，分别为

KCN=\sum_{i=2}^{n} i = \frac{(n+2)(n-1)}{2} \approx \frac{n^2}{2}

RMN=\sum_{i=2}^{n} (i+1) = \frac{(n+4)(n-1)}{2} \approx \frac{n^2}{2}

若待排序序列中出现各种可能排列的概率相同，则可取上述最好情况和最坏情况的平均情况。在平均情况下，直接插入排序关键字的比较次数和记录移动次数均约为 $\frac{n^2}{4}$ 。

综上，直接插入排序的时间复杂度为 $O(n^2)$ 。

从空间上来看，直接插入排序只需要一个辅助空间r[0]，所以空间复杂度为O(1)。

1.4、算法特点

直接插入排序的特点为：

稳定排序。
算法简单，且易实现。
适用于链式存储结构。在单链表上无需移动记录，只需修改相应的指针。
更适合于初始记录基本有序（正序）的情况，当初始记录无序，n较大时，此算法时间复杂度较高，不宜采用。

二、折半插入排序

折半插入排序（Binary Insertion Sort）采用折半查找法查找当前待排序记录在有序区中的插入位置。

2.1、算法步骤

折半插入排序的算法步骤为：

设待排序记录存放在数组r[1…n]中，初始有序区为r[1]
循环n-1次，执行以下操作：
- 使用折半查找法，在有序区r[1…i-1]中查找r[i]的插入位置
- 将r[i]插入到表长为i-1的有序区r[1…i-1]中。

2.2、算法描述

// 对顺序表L进行折半插入排序
void BInsertSort(SqList &L) {
    // 长度为n的表，要进行n-1趟排序
    for(i=2;i<=L.length;++i) {
        // 将待插入记录暂存到监视哨中
        L.r[0]=L.r[i];
        // 设置查找区间初值
        low=1; high=i-1;

        // 在有序区r[low..high]中，折半查找r[i]的插入位置
        while(low<=high) {
            // 折半
            m=(low+high)/2;
            // 插入位置在前一子表
            if(L.r[0].key<L.r[m].key) high=m-1;
            // 插入位置在后一子表
            else low=m+1;
        }

        // 记录后移
        for(j=i-1;j>=high+1;--j) {
            L.r[j+1]=L.r[j];
        }

        // 将r[0]即原r[i]，插入到正确位置
        L.r[high+1]=L.r[0];
    }
}

2.3、算法分析

从时间上来看，折半查找比顺序查找快，所以就平均性能来说，折半插入排序优于直接插入排序。

折半插入排序所需要的关键字比较次数与待排序序列的初始排列无关，仅依赖于记录的个数。不论初始序列情况如何，在插入第i个记录时，需要经过 $\lfloor log_2 i \rfloor + 1$ 次比较，才能确定它应插入的位置。所以当记录的初始排列为正序或接近正序时，直接插入排序比折半插入排序执行的关键字比较次数要少。折半插入排序的对象移动次数与直接插入排序相同，依赖于对象的初始排列。

在平均情况下，折半插入排序仅减少了关键字间的比较次数，而记录的移动次数不变。因此，折半插入排序的时间复杂度仍为 $O(n^2)$ 。

从空间上来看，折半插入排序只需要一个记录的辅助空间r[0]，所以空间复杂度为O(1)。

2.4、算法特点

折半插入排序的特点为：

稳定排序。
不适用于链式结构。因为为要进行折半查找，所以只能用于顺序结构。
适合初始记录无序、n较大时的情况。

三、希尔排序

希尔排序（Shell’s Sort）又称“缩小增量排序”（Diminishing Increment Sort），由D.L.希尔（D.L.Shell）于1959年提出而得名。

希尔排序是对直接插入排序算法的优化。当待排序的记录个数较少，且待排序序列的关键字基本有序时，采用直接插入排序，效率会很高。希尔排序正式基于以上两点，从“减少记录个数”和“序列基本有序”两个方面，对直接插入排序进行了改进。

希尔排序的主要思想是分组插入。先将整个待排序记录序列分割成几组，对每个组分别进行直接插入排序，减少参与直接插入排序的数据量，然后增加每组的数据量，重新分组。这样，当经过几次分组排序后，整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。希尔排序对记录的分组，不是简单地“逐段分割”，而是将相隔某个“增量”的记录分成一组。

3.1、算法步骤

希尔排序的算法步骤为：

第一趟取增量 $d_1(d_1<n)$ ，把全部记录分成 $d_1$ 个组，所有间隔为 $d_1$ 的记录分在同一组，并在每个组中进行直接插入排序。
第二趟取增量 $d_2(d_2<d_1)$ ，重复上述的分组和排序。
依次类推，直到所取的增量 $d_t=1(d_t<d_{t-1}<...<d_2<d_1)$ ，所有记录在同一组中进行直接插入排序为止。

如下图，是对一组关键字序列为 $\{49,38,65,97,76,13,27, \overline{49}, 55, 04\}$ 的待排序记录，进行希尔排序的过程（每趟排序的增量分别为5、3和1）。

第一趟排序，取增量 $d_1=5$ ，所有间隔为5的记录分在同一组，全部记录分成5组 $(49,13)、(38,27)、 (65,\overline{49})、 (97,55)、 (76,04)$ ，在各个组中分别进行直接插入排序，排序结果为 $\{13,27,\overline{49},55,04,49,38, 65, 97, 76\}$ 。

第二趟排序，取增量 $d_2=3$ ，所有间隔为3的记录分在同一组，全部记录分成3组 $(13,55,38, 76)、 (27,04,65,)、 (\overline{49},49,97)$ ，在各个组中分别进行直接插入排序，排序结果为 $\{13,04,\overline{49},38,27,49,55, 65, 97, 76\}$ 。

第三趟排序，取增量 $d_3=1$ ，对整个序列进行直接插入排序，排序完成。

3.2、算法描述

// 对顺序表L进行一趟增量是k的希尔插入排序
void ShellInsert(SqList &L, int dk) {
    // 对dk个组分别进行直接插入排序
    for(i=1+dk;i<=L.length;++i) {
        // r[i]小于增量有序子区的最大值，需将L.[i]插入到增量有序子区
        if(L.r[i].key<L.r[i-dk].key) {
            // 将r[i]暂存到r[0]中
            L.r[0]=L.r[i];
            
            // 查找r[i]的插入位置，同时后移记录
            for(j=i-dk; L.r[0].key<L.r[j].key && j>0; j-=dk) {
                // 记录后移
                L.r[j+dk]=L.r[j];
            }
            
            // 将r[0]即原r[i]，插入到正确位置
            L.r[j+dk]=L.r[0];
        }
    }
}

// 对顺序表L，按增量序列dt[0..t-1]，进行t趟希尔插入排序
void ShellSort(SqList &L, int dt[], int t) {
    for(k=0;k<t;++k)
        // 一趟增量为dt[k]的希尔插入排序
        ShellInsert(L,dt[k]);
}

在该算法中，预设好的增量序列保存在数组dt[0…t−1]中，整个希尔排序算法需执行t趟。

直接插入排序可以看成一趟增量是1的希尔插入排序。一趟增量是k的希尔插入排序算法，可以通过改写直接插入排序的算法得到，具体改写主要有两处：

前后记录位置的增量是dk，而不是1；
r[0]只是暂存单元，不是哨兵。当j<=0时，插入位置已找到。

3.3、算法分析

从时间上来看，当增量大于1时，关键字较小的记录就不是一步一步地挪动，而是跳跃式地移动，从而使得在进行最后一趟增量为1的直接插入排序时，序列已基本有序，只要做记录的少量比较和移动即可完成排序，因此希尔排序的时间复杂度较直接插入排序低。

具体分析希尔排序的时间复杂度是一个复杂的问题。因为希尔排序的时间复杂度是所取“增量”序列的函数，这涉及一些数学上尚未解决的难题。因此，到目前为止尚未有人求得一种最好的增量序列，但大量的研究已得出一些局部的结论。

比如有人指出，当增量序列为 $dt[k]=2^{t-k+1}-1$ 时，希尔排序的时间复杂度为 $O(n^{3/2})$ ，其中t为排序趟数， $1 \leq k \leq t \leq \lfloor log_2 (n+1) \rfloor$ 。还有人在大量的实验基础上推出：当n在某个特定范围内，希尔排序所需的比较和移动次数约为 $n^{1.3}$ ，当 $n \rightarrow \infty$ 时，比较和移动次数可减少到 $n(log_2 n)^2$ 。