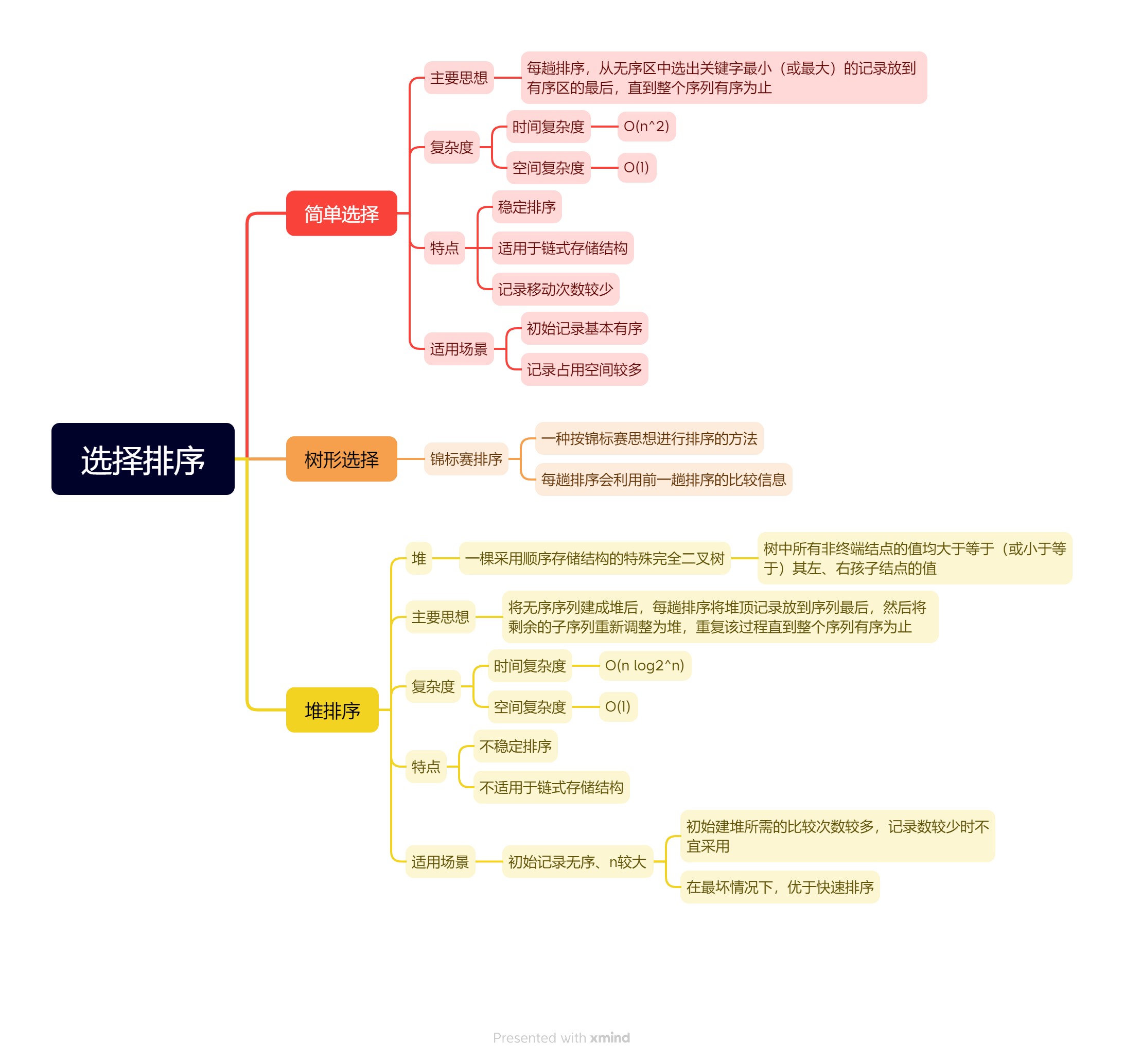
数据结构：选择排序

选择排序的基本思想是：每趟排序，从无序区中选出关键字最小（或最大）的记录放到有序区的最后，直到整个序列有序为止。常用的选择排序算法是简单选择排序和堆排序。

一、简单选择排序

简单选择排序（Simple Selection Sort）也称作直接选择排序。

1.1、算法步骤

简单选择排序算法的步骤为：

  • 设待排序记录存放在数组r[1…n]中。
  • 第一趟排序，从r[1]开始，通过n-1次比较，从n个记录中选出关键字最小的记录，记为r[k]，交换r[1]和r[k]。
  • 第二趟排序，从r[2]开始，通过n-2次比较，从n-1个记录中选出关键字最小的记录，记为r[k]，交换r[2]和r[k]。
  • 依次类推，第i趟排序，从r[i]开始，通过n-i次比较，从n-i+1个记录中选出关键字最小的记录，记为r[k]，交换r[i]和r[k]。
  • 经过n-1趟排序后，排序完成，得到一个有序序列。

如下图，是对一组关键字序列为{49,38,65,97,49‾,76,13,27}\{49, 38, 65, 97, \overline{49}, 76, 13, 27\}的待排序记录，进行简单选择排序的过程。

image-20240528081404597

1.2、算法描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 对顺序表L进行简单选择排序
void SelectSort(SqList &L) {
    // 在L.r[i..L.length]中选择关键字最小的记录
    for(i=1;i<L.length;++i) {
        k=i;
        for(j=i+1;j<=L.length;++j)
            // k指向此趟排序中关键字最小的记录
            if(L.r[j].key<L.r[k].key) k=j;
        // 交换r[i]与r[k]
        if(k!=i) {
            t=L.r[i];
            L.r[i]=L.r[k];
            L.r[k]=t;
        }
    }
}

1.3、算法分析

从时间上来看，简单选择排序所需进行记录移动的次数较少。最好情况（正序）：不移动；最坏情况（逆序）：移动3(n−1)次。然而，无论记录的初始排列如何，所需进行的关键字间的比较次数相同，均为

KCN=∑i=1n−1n−i=n(n−1)/2≈n2/2KCN=\sum_{i=1}^{n-1} n-i = n(n-1)/2 \approx n^2/2

因此，简单选择排序的时间复杂度是O(n2)O(n^2)。

从空间上来看，只在两个记录交换时需要一个辅助空间，所以空间复杂度为O(1)。

1.4、算法特点

简单选择排序算法的特点为：

  • 稳定排序。就选择排序方法本身来讲，它是一种稳定的排序方法，但前面的示例所表现出来的现象是不稳定的，这是因为上述实现选择排序的算法采用“交换记录”的策略所造成的，改变这个策略，可以写出稳定”的选择排序算法。
  • 可用于链式存储结构。
  • 记录移动次数较少。当每个记录占用的空间较多时，此方法比直接插入排序快。

二、树形选择排序

树形选择排序（Tree Selection Sort），又称锦标赛排序（Tournament Sort），是一种按照锦标赛的思想进行选择排序的方法。

2.1、锦标赛思想

简单选择排序的主要操作是进行关键字间的比较，因此改进简单选择排序应从如何减少“比较”出发考虑。显然，在n个关键字中选出最小值，至少要进行n−1次比较，然而，继续在剩余的n−1个关键字中选择次小值并非一定要进行n−2次比较，若能利用前n−1次比较所得信息，则可减少以后各趟选择排序中所进行的比较次数。体育比赛中的锦标赛便是这种思想。

比如，在8个运动员中决出前3名至多需要11场比赛，而不是7+6+5=18场比赛（它的前提是，若乙胜丙，甲胜乙，则认为甲必能胜丙）。如下图所示，8个选手（最低层的叶子结点）之间经过第一轮的4场比寒之后选拔出4个优胜者，他们分别是“CHA”、“BAO”、“DIAO”和“WANG”，然后经过两场半决赛和一场决赛之后，选拔出冠军“BAO”。

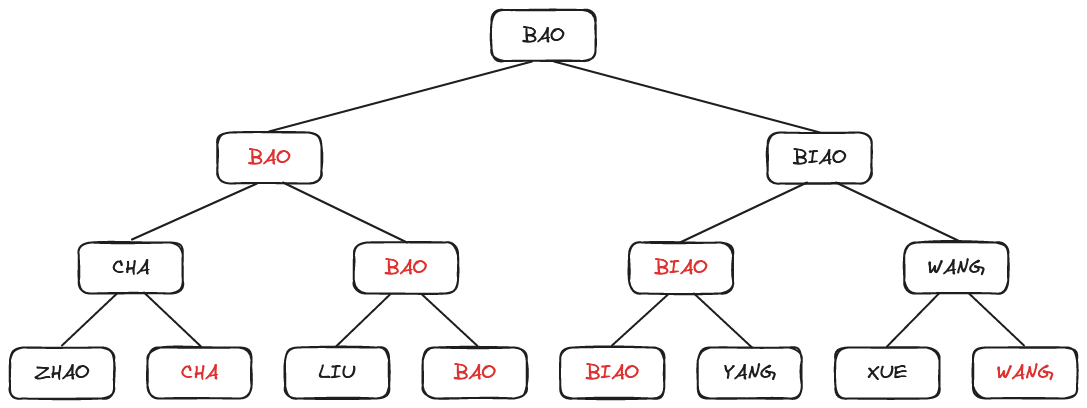
image-20240529074755213

显然，按照锦标赛的传递关系，亚军只能产生于分别在决赛、半决赛和第一轮比赛中输给冠军的选手中。由此，在经过“CHA”和“LIU”、“CHA”和“DIAO”的两场比赛之后，选拔出亚军“CHA”。

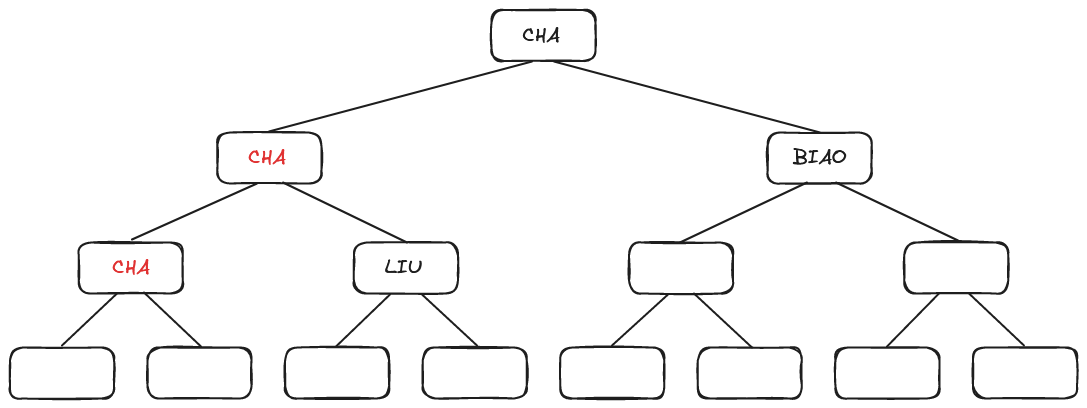
image-20240529081859212

同理，选拔季军的比赛只要在“ZHAO”、“LIU”和“DIAO”3个选手之间进行即可。

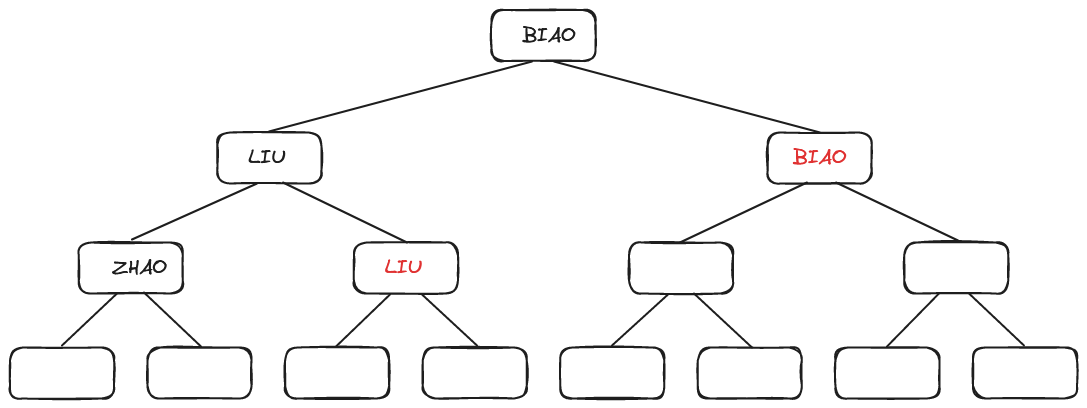
image-20240529082006532

2.2、树形选择排序

按照锦标赛思想，可导出树形选择排序：先对n个记录的关键字进行两两比较，然后在其中$\lceil n/2 \rceil $个较小者之间再进行两两比较，如此重复，直至选出关键字最小的记录为止。该过程可用一棵有n个叶子结点的完全二叉树表示。例如，下图中的二叉树表示从8个关键字中选出最小关键字的过程。二叉树的8个叶子结点依次存放排序之前的8个关键字，每个非终端结点中的关键字均等于其左、右孩子结点中较小的关键字，根结点中的关键字即为叶子结点中的最小关键字。

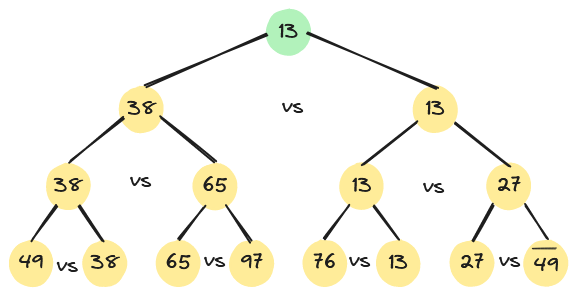
image-20240529090838074

在输出最小关键字之后，根据关系的可传递性，欲选出次小关键字，仅需将叶子结点中的最小关键字13改为“最大值”，然后从该叶子结点开始，和其左（或右）兄弟的关键字进行比较，修改从该叶子结点到根的路径上各结点的关键字，则根结点的关键字即为次小关键字。

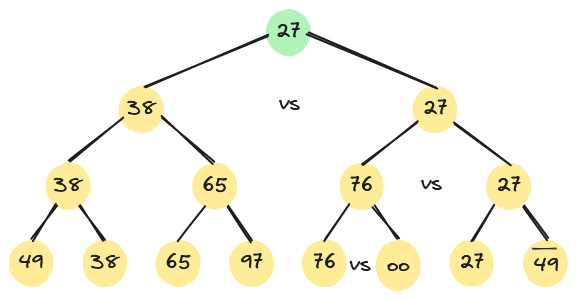
image-20240529090032330

按照上述过程，在经过n趟排序后，就能得到一个有序序列。

由于含有n个叶子结点的完全二叉树的深度为⌈log2n⌉+1\lceil log_2n \rceil + 1，因此在树形选择排序中，除了第一趟排序外，其余每趟排序仅需进行⌈log2n⌉\lceil log_2n \rceil次比较，因此，它的时间复杂度为O(nlog2n)O(nlog_2n)。但是，这种排序方法尚有辅助存储空间较多、和“最大值”进行多余比较等缺点。

为了改进树形选择排序的缺点，威廉姆斯（J.Willioms）在1964年提出了另一种形式的树形选择排序——堆排序。

三、堆排序

堆排序（Heap Sort）是一种树形选择排序，其主要思想是，在排序过程中，将待排序记录r[1…n]看成是一棵完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的内在关系，在当前无序的序列中选择关键字最大（或最小）的记录。

3.1、堆的定义

堆是含有n个元素的序列{k1,k2,...,kn}\{k_1,k_2,...,k_n\}，其元素满足如下条件：

ki≥k2i且ki≥K2i+1(1≤i≤⌊n/2⌋)k_i \ge k_{2i}且k_i \ge K_{2i+1} \quad (1 \le i \le \lfloor n/2 \rfloor)

或：

ki≤k2i且ki≤K2i+1(1≤i≤⌊n/2⌋)\quad k_i \le k_{2i}且k_i \le K_{2i+1} \quad (1 \le i \le \lfloor n/2 \rfloor)

若将和此序列对应的一维数组（即以一维数组做此序列的存储结构）看成是一个完全二叉树，则堆实质上是一棵特殊的完全二叉树：树中所有非终端结点的值均大于等于（或小于等于）其左、右孩子结点的值。

例如，关键字序列{96,83,27,38,11,09}\{96, 83, 27, 38, 11, 09\}和{12,36,24,85,47,30,53,91}\{12, 36, 24, 85, 47, 30, 53, 91\}分别满足条件ki≥k2i且ki≥K2i+1(1≤i≤⌊n/2⌋)k_i \ge k_{2i}且k_i \ge K_{2i+1} (1 \le i \le \lfloor n/2 \rfloor)和条件ki≤k2i且ki≤K2i+1(1≤i≤⌊n/2⌋)\quad k_i \le k_{2i}且k_i \le K_{2i+1} (1 \le i \le \lfloor n/2 \rfloor)，故它们均为堆，对应的完全二叉树如下图所示。在下图（a）中，所有非终端结点的值均大于等于其左、右孩子结点的值，这样的堆我们称之为“大根堆”。在下图（b）中，所有非终端结点的值均小于等于其左、右孩子结点的值，这样的堆我们称之为“小根堆”。

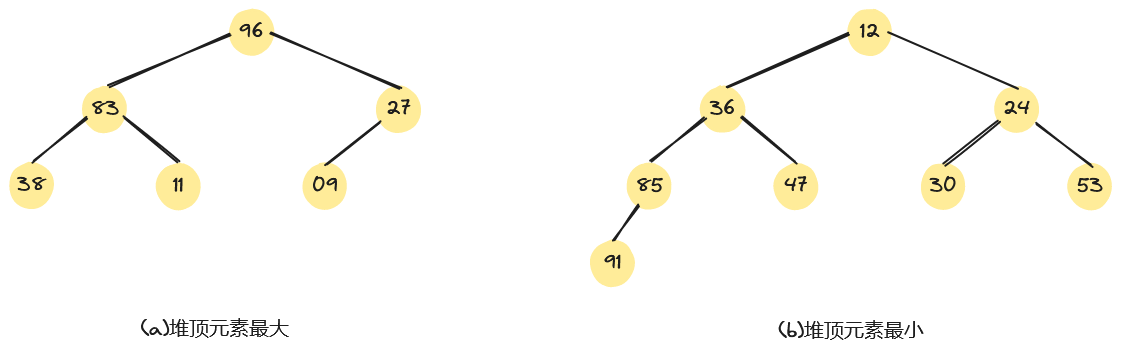
image-20240530084704781

堆排序利用大根堆（或小根堆）堆顶记录的关键字最大（或最小）这一特征，使得在当前无序的序列中选择关键字最大（或最小）的记录变得简单。接下来，我们以大根堆为例，讨论如何进行堆排序。

3.2、算法步骤

堆排序的步骤如下：

  • 按堆的定义将待排序序列r[1…n]调整为大根堆（此过程称为建初堆），交换r[1]和r[n]，则r[n]为关键字最大的记录。
  • 将r[1…n-1]重新调整为大根堆，交换r[1]和r[n-1]，则r[n-1]为关键字次大的记录。
  • 循环n-1次，直到交换了r[1]和r[2]为止，得到一个递增的有序序列r[1…n]。

可见，实现堆排序需要解决如下两个问题。

  • 建初堆：如何将一个无序序列建成一个堆？
  • 调整堆：在堆顶元素改变之后，如何将剩余元素调整成为一个新堆？

因为建初堆要用到调整堆的操作，所以下面先讨论调整堆的实现。

3.2.1、调整堆

我们先看一个具体示例。如下，左图是一个大根堆，将堆顶元素97和堆中最后一个元素38交换。

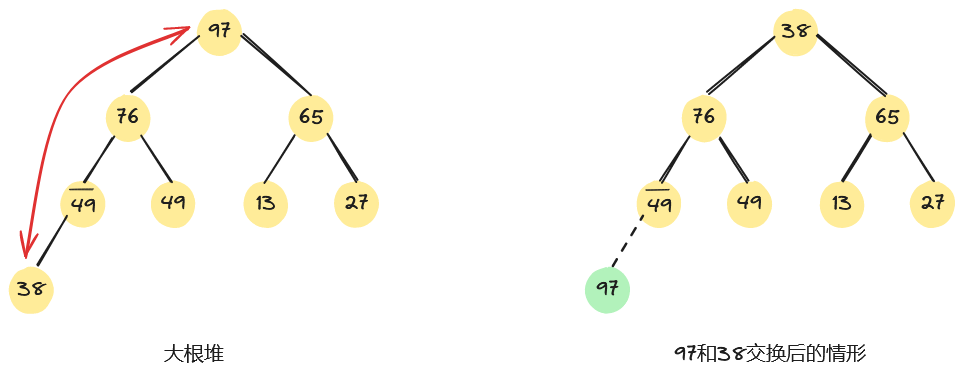
image-20240606075201098

此时除根结点外，其余结点均满足堆的性质，因此需从根节点开始，从上到下进行一条路径上的结点调整。首先，将堆顶元素38和其左、右子树根结点的值进行比较，由于左子树根结点的值大于右子树根结点的值且大于根结点的值，因此将38和76交换；因为38替代了76之后破坏了左子树的“堆”，所以需进行相同的调整，直至叶子结点，整个过程如下所示。

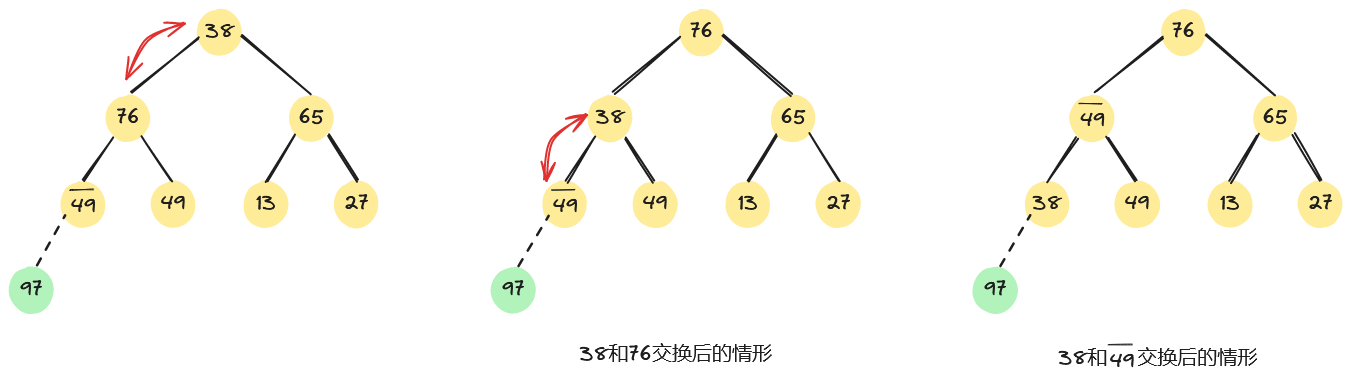
image-20240606075924309

重复上述过程，将堆顶元素76和堆中最后一个元素27交换，进行相应调整后，会得到如下图所示的堆。

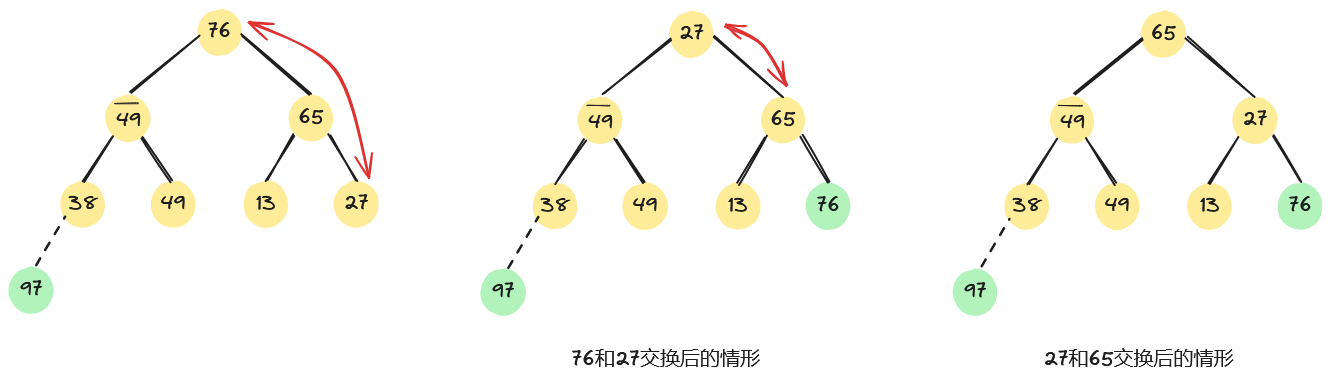
image-20240606080723828

上述过程就像过筛子一样，把较小的关键字逐层筛下去，而将较大的关键字逐层选上来。因此，称此方法为“筛选法”。现假设r[s+1…m]已经是堆，按“筛选法”将r[s…m]调整为以r[s]为根的大根堆，其算法步骤是：

  • 从r[2s]和r[2s+1]中选出关键字较大者，假设r[2s]的关键字较大，比较r[s]和r[2s]的关键字。
    • 若r[s].key≥r[2s].keyr[s].key \ge r[2s].key，说明以r[s]为根的子树已经是大根堆，不必做任何调整。
    • 若r[s].key<r[2s].keyr[s].key \lt r[2s].key，则交换r[s]和r[2s]。交换后，以r[2s+1]为根的子树仍是堆，如果以r[2s]为根的子树不是堆，则重复上述过程，将以r[2s]为根的子树调整为堆，直至进行到叶子结点为止。

相应的算法描述为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 假设r[s+1..m]已经是堆，将r[s..m]调整为以r[s]为根的大根堆
void HeapAdjust(SqList &L, int s, int m) {
    rc=L.r[s];

    // 沿关键字较大的孩子结点向下筛选，直到叶子结点
    for(j=2*s;j<=m;j*=2) {
        // j为r[2s]和r[2s+1]中关键字较大者的下标
        if(j<m && L.r[j].key<L.r[j+1].key ) ++j;
        
        // r[s].key>=r[2s].key，无需进行交换
        if(rc.key>=L.r[j].key) break;
        
        // r[s].key<r[2s].key，交换r[s]和r[2s]
        L.r[s]=L.r[j];
        // rc应插入在位置s上
        s=j;
    }

    // 插入rc
    L.r[s]=rc;
}

3.2.2、建初堆

将一个无序序列调整为堆，必须将其所对应的完全二叉树中以每一结点为根的子树都调整为堆。

显然，只有一个结点的树必是堆，而在完全二叉树中，所有序号大于$\lfloor n/2 \rfloor 的结点都是叶子，因此以这些结点为根的子树均已是堆。这样，只需利用筛选法，从最后一个非终端结点的结点都是叶子，因此以这些结点为根的子树均已是堆。这样，只需利用筛选法，从最后一个非终端结点\lfloor n/2 \rfloor 开始，依次将序号为开始，依次将序号为\lfloor n/2 \rfloor , \lfloor n/2 \rfloor - 1,…,1$的结点作为根的子树都调整为堆即可。

建初堆的算法步骤为：对于无序序列r[1…n]，从i=n/2开始到i=1，反复调用HeapAdjust(L,i,n)，依次将以r[i],r[i−1],...,r[1]r[i],r[i-1],...,r[1]为根的子树调整为堆。相应的算法描述为：

1
2
3
4
5
6
7
8
// 把无序序列L.r[1..n]建成大根堆
void CreatHeap(SqList &L) {
    n=L.length;

    // 反复调用HeapAdjust
    for(i=n/2;i>0;--i)
        HeapAdjust(L,i,n);
}

如下图，是将一组无序序列{49,38,65,97,76,13,27,49‾}\{49, 38, 65, 97, 76, 13, 27, \overline{49}\}，调整为一个大根堆的建堆过程。从无序序列的最后一个非终端结点开始筛选，即从第4个元素97开始，由于97>49，无需交换。同理，第3个元素65不小于其左、右子树根的值，仍无需交换。而第2个元素38<97，需要进行交换。根元素49<97，也需进行交换。

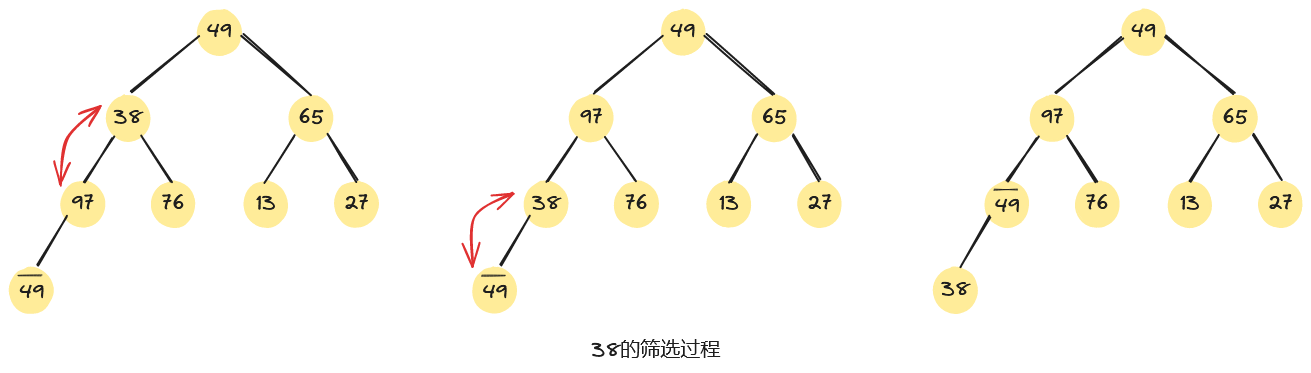
image-20240604083257505

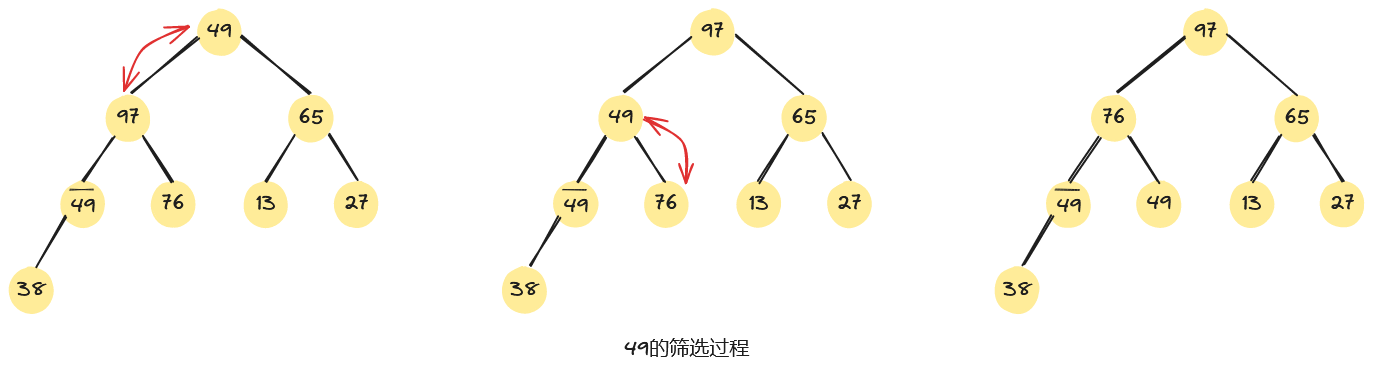
image-20240604083041741

3.3、算法实现

根据前面堆排序算法步骤的描述，可知堆排序就是将无序序列建成初堆以后，反复进行交换和堆调整。在建初堆和调整堆算法实现的基础上，可以给出堆排序算法的实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 对顺序表L进行堆排序
void HeapSort(SqList &L) {
    // 把无序序列L.r[1..L.length]建成大根堆
    CreatHeap(L);

    // 进行n-1次交换和堆调整
    for(i=L.length;i>1;--i) {
        // 将堆顶记录和当前未经排序的子序列L.r[1..i]中的最后一个记录互换
        x=L.r[1];
        L.r[1]=L.r[i];
        L.r[i]=x;

        // 将L.r[1..i-1]重新调整为大根堆
        HeapAdjust(L,1,i-1);
    }
}

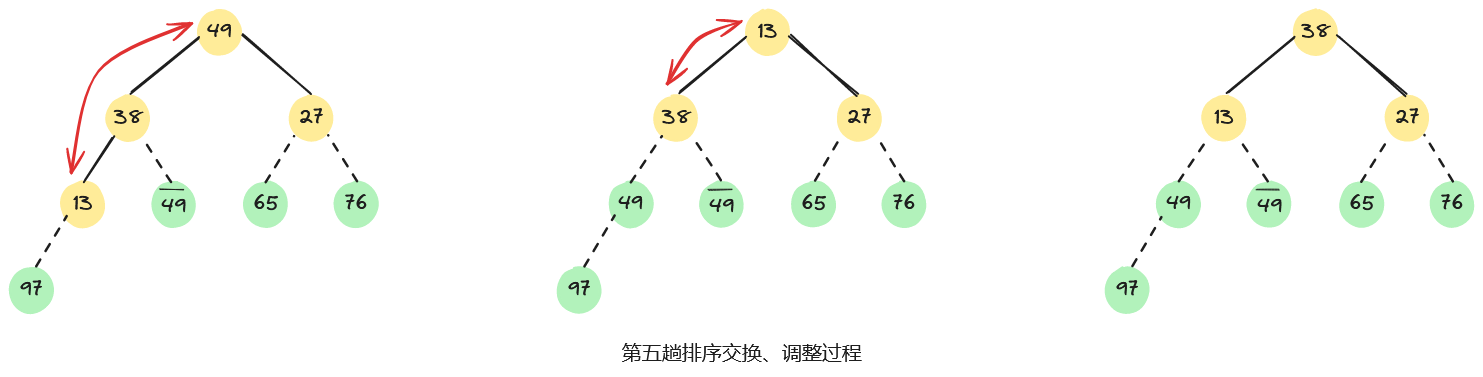
例如，已知无序序列{49,38,65,97,76,13,27,49‾}\{49, 38, 65, 97, 76, 13, 27, \overline{49}\}，用堆排序法进行排序的过程为：首先，将无序序列建初堆；然后，在初始大根堆的基础上，反复交换堆顶元素和最后一个元素，并重新调整堆；直至最后得到一个有序序列，整个堆排序过程如下图所示。

image-20240605082620666

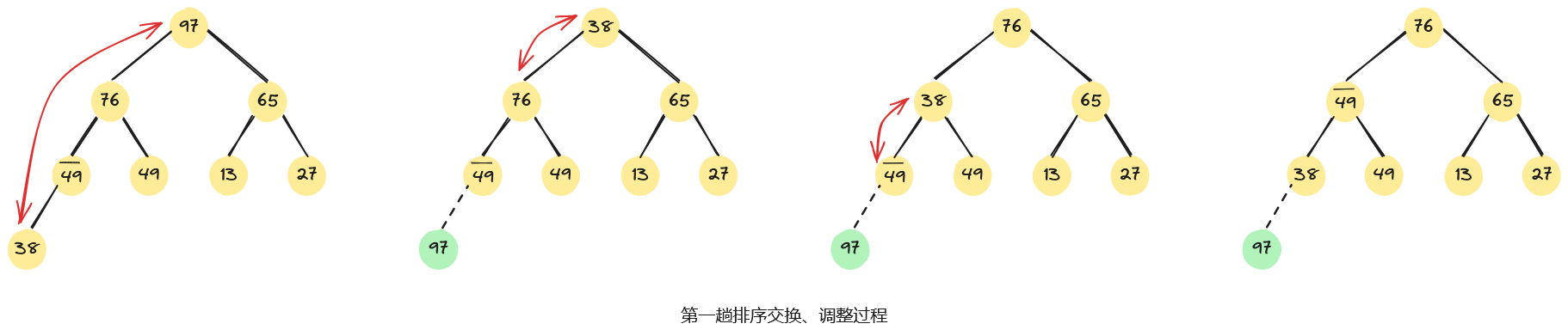
image-20240605083511845

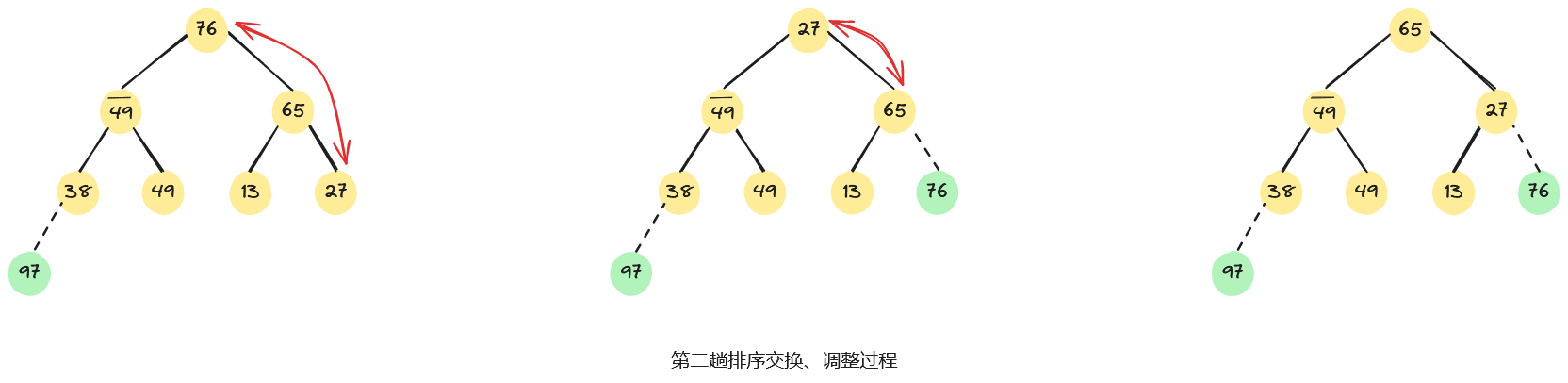
image-20240605084100284

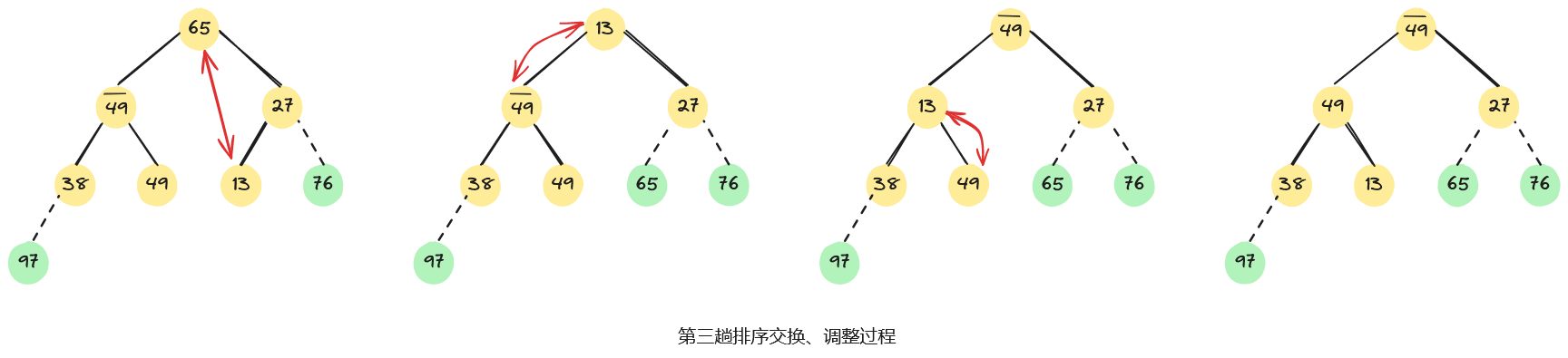
image-20240605084541135

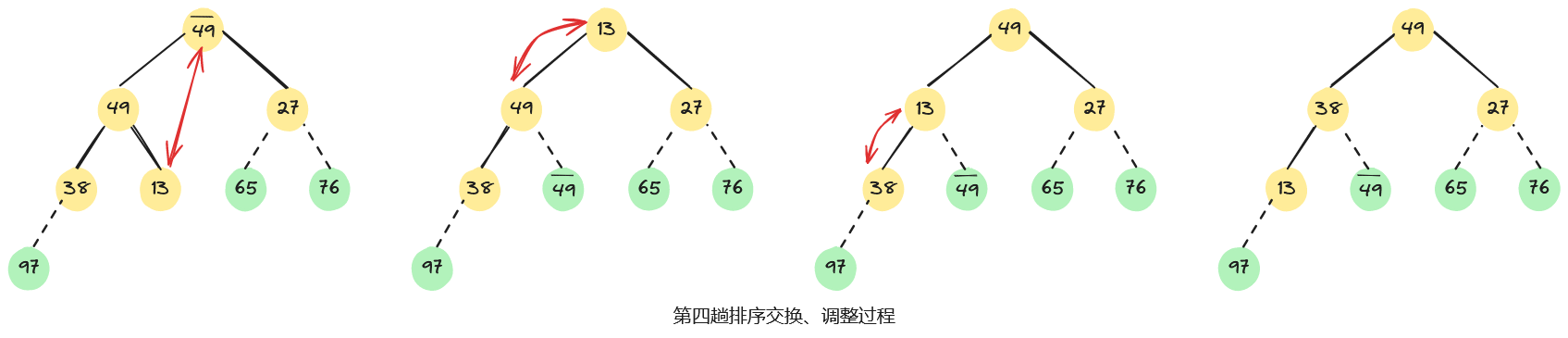
image-20240605085007200

image-20240605085435182

image-20240605090238486

image-20240605090640281

3.4、算法分析

从时间上来看，堆排序的运行时间主要耗费在建初堆和调整建新堆时进行的反复筛选。设有n个记录的初始序列所对应的完全二叉树的深度为h。

建初堆时，每个非终端结点都要自上而下进行筛选。由于第i层上的结点数小于等于2i−12^{i-1}，且第i层上的结点最大下移深度为h−i，而每下移一层要做两次比较，因此建初堆时关键字总的比较次数为

∑i=h−112i−1∗2(h−i)=∑i=h−112i∗(h−i)=∑j=1h−12h−j∗j≤2n∑j=1h−1j/2j≤4n\sum_{i=h-1}^{1} 2^{i-1} * 2(h-i) = \sum_{i=h-1}^{1} 2^i * (h-i) = \sum_{j=1}^{h-1} 2^{h-j} * j \le 2n \sum_{j=1}^{h-1} j/2^j \le 4n

调整建新堆时，要做n−1次筛选，每次筛选都要将根结点下移到合适的位置。有n个结点的完全二叉树，其深度为⌊log2n⌋+1\lfloor log_{2}{n} \rfloor + 1，则重建堆时关键字总的比较次数不超过

2(⌊log2(n−1)⌋+⌊log2(n−2)⌋+...+log22)<2n(⌊log2n⌋)2(\lfloor log_{2}{(n-1)} \rfloor + \lfloor log_{2}{(n-2)} \rfloor + ...+ log_{2}{2}) \lt 2n(\lfloor log_{2}{n} \rfloor)

综上，堆排序在最坏情况下，时间复杂度为也O(nlog2n)O(n log_{2}{n})。实验研究表明，堆排序的平均性能接近于最坏性能。

从空间上来看，仅需一个记录大小供交换用的辅助存储空间，所以空间复杂度为O(1)。

3.5、算法特点

堆排序算法的特点为：

  • 不稳定排序。
  • 不适用于链式结构。因为堆是一棵采用顺序存储结构的特殊完全二叉树。
  • 记录数较多时较为高效。初始建堆所需的比较次数较多，因此记录数较少时不宜采用。堆排序在最坏情况下时间复杂度为O(nlog2n)O(nlog_{2}{n)}，相对于快速排序最坏情况下的O(n2)O(n^2)而言是一个优势。

四、小结

img

五、参考

《数据结构（C语言版 第2版）》

《数据结构 自考02331》

数据结构
#数据结构
数据结构：选择排序
https://kuberxy.github.io/2024/05/12/数据结构：选择排序/
作者
Mr.x
发布于
2024年5月12日
许可协议