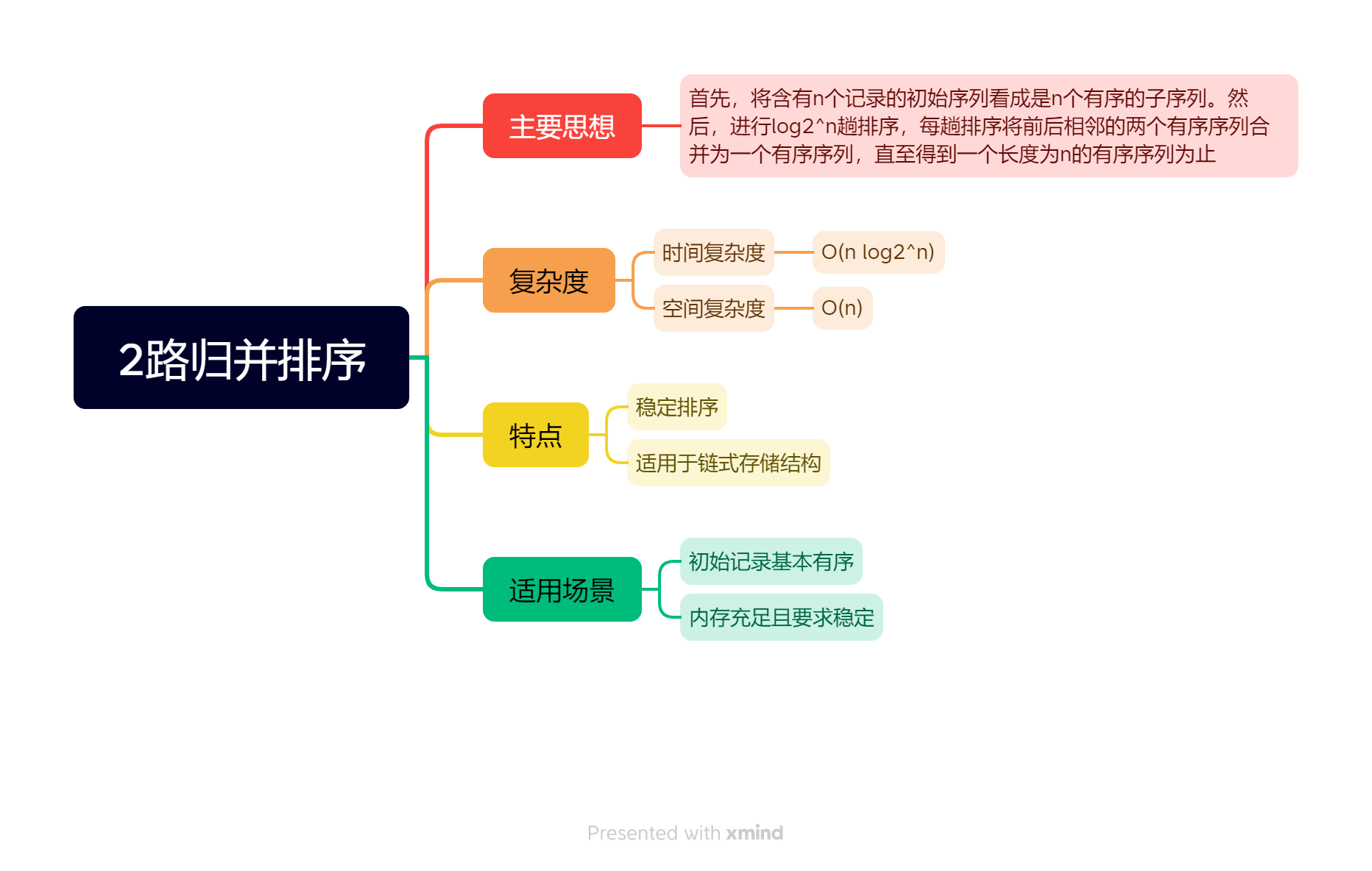
数据结构:归并排序
归并排序(Merging Sort)就是将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并成一个有序表的过程称为2-路归并,2-路归并是最简单、最常用的归并排序算法,也是本篇文章主要讨论的内容。
一、算法思想
2-路归并排序算法的思想是:将含有n个记录的初始序列看成是n个有序的子序列,每个子序列的长度为1。两两归并,得到个长度为2或1的有序子序列;再两两归并,……,如此重复,直至得到一个长度为n的有序序列为止。
如下图,是将一组关键字序列为的待排序记录,看成是7个长度为1的子序列后,进行2-路归并排序的过程。
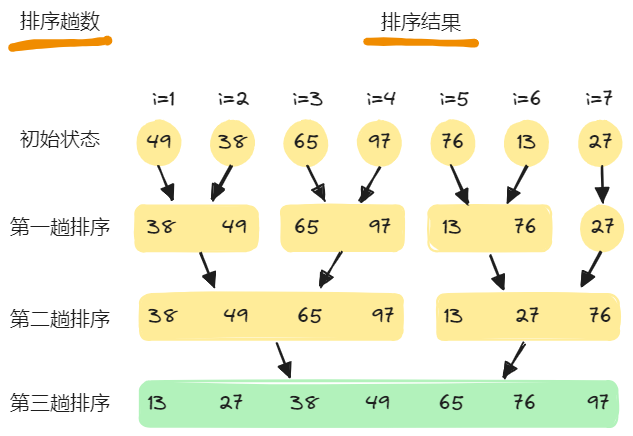
在2-路归并排序中,每趟排序的核心操作是,将待排序序列中前后相邻的两个有序序列合并为一个有序序列。该操作的算法步骤为:设两个有序表存放在同一数组中相邻的位置(R[low…mid]和R[mid+1…high])上,每次分别从两个表中取出一个记录进行关键字比较,将较小者放入T[low…high]中,重复此过程,直至其中一个表为空,最后将另一非空表中余下的部分直接复制到T中。相应的算法描述如下:
1 | |
二、算法步骤
与快速排序类似,2-路归并排序也可以利用递归实现子序列的划分。首先把整个待排序序列划分为两个长度大致相等的子序列,然后对这两个子序列分别递归地进行排序,最后再把它们合并。
2-路归并排序算法的步骤为:将R[low…high]中的记录归并排序后放入T[low…high]中。当序列长度等于1时,递归结束,否则:
- 将当前序列一分为二,求出分裂点mid;
- 对子序列R[low…mid]递归,进行归并排序,结果放入T[low…mid]中;
- 对子序列R[mid+1…high]递归,进行归并排序,结果放入T[mid+1…high]中;
- 调用算法Merge,将有序的两个子序列R[low…mid]和R[mid+1…high]归并为一个有序的序列T[low…high]。
如下图,是对一组关键字序列为的待排序记录,进行2-路归并排序的过程。
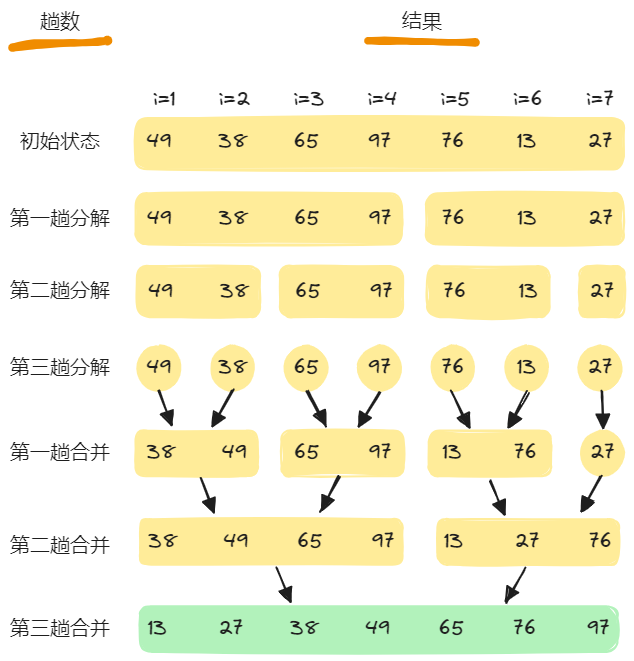
三、算法描述
1 | |
下图,是对一组关键字序列为的待排序记录,调用Msort函数的过程。
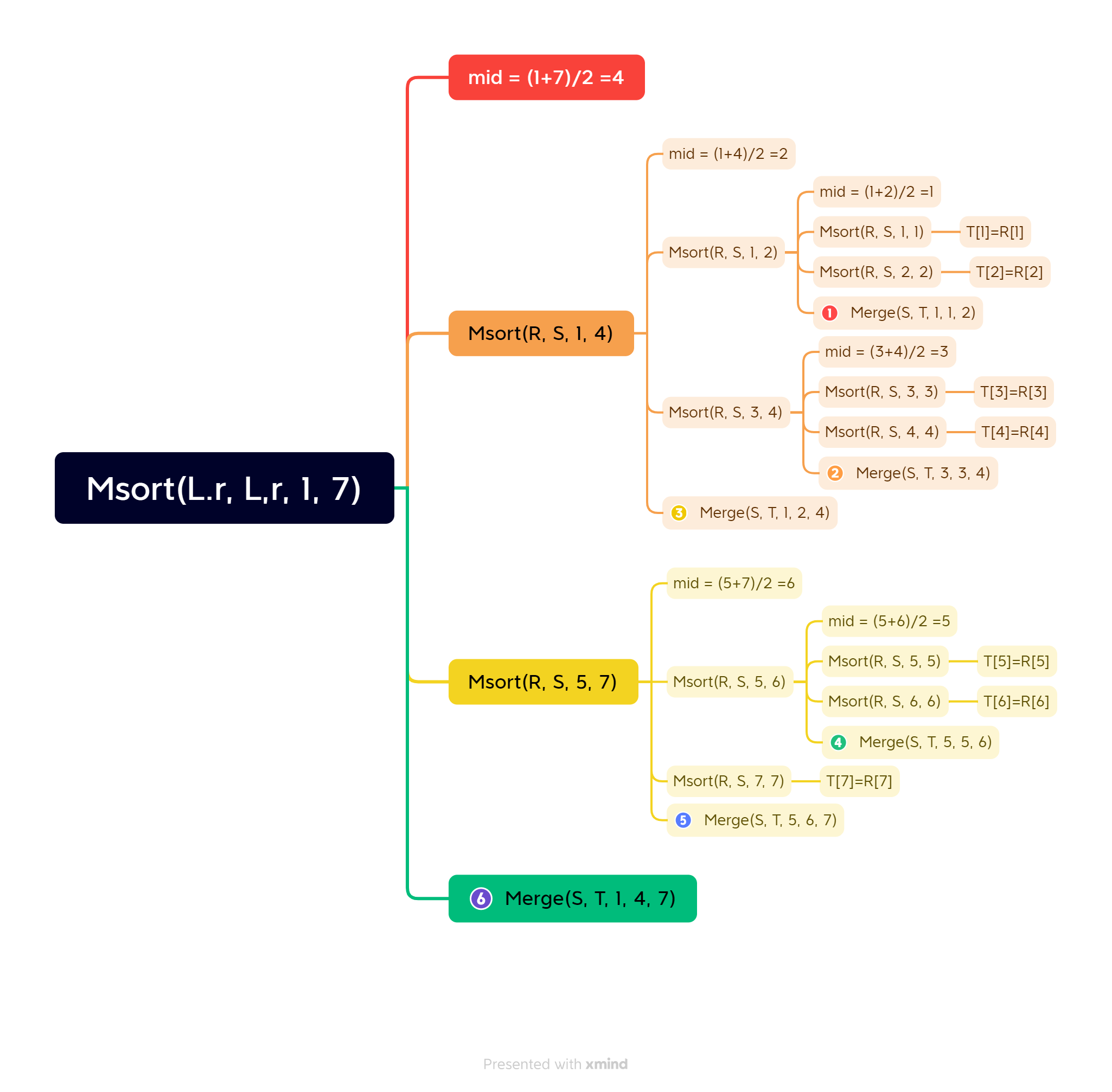
四、算法分析
从时间上来看,当有n 个记录时,需进行趟排序。每一趟排序,关键字比较次数不超过n ,元素移动次数都是n 。因此,归并排序的时间复杂度为。
从空间上来看,用顺序表实现归并排序时,需要和待排序记录个数相等的辅助存储空间,所以空间复杂度为O(n)。
五、算法特点
归并排序算法的特点为:
- 稳定排序。
- 适用于链式结构,且不需要附加存储空间,但递归实现时仍需要开辟相应的递归工作栈。
六、总结