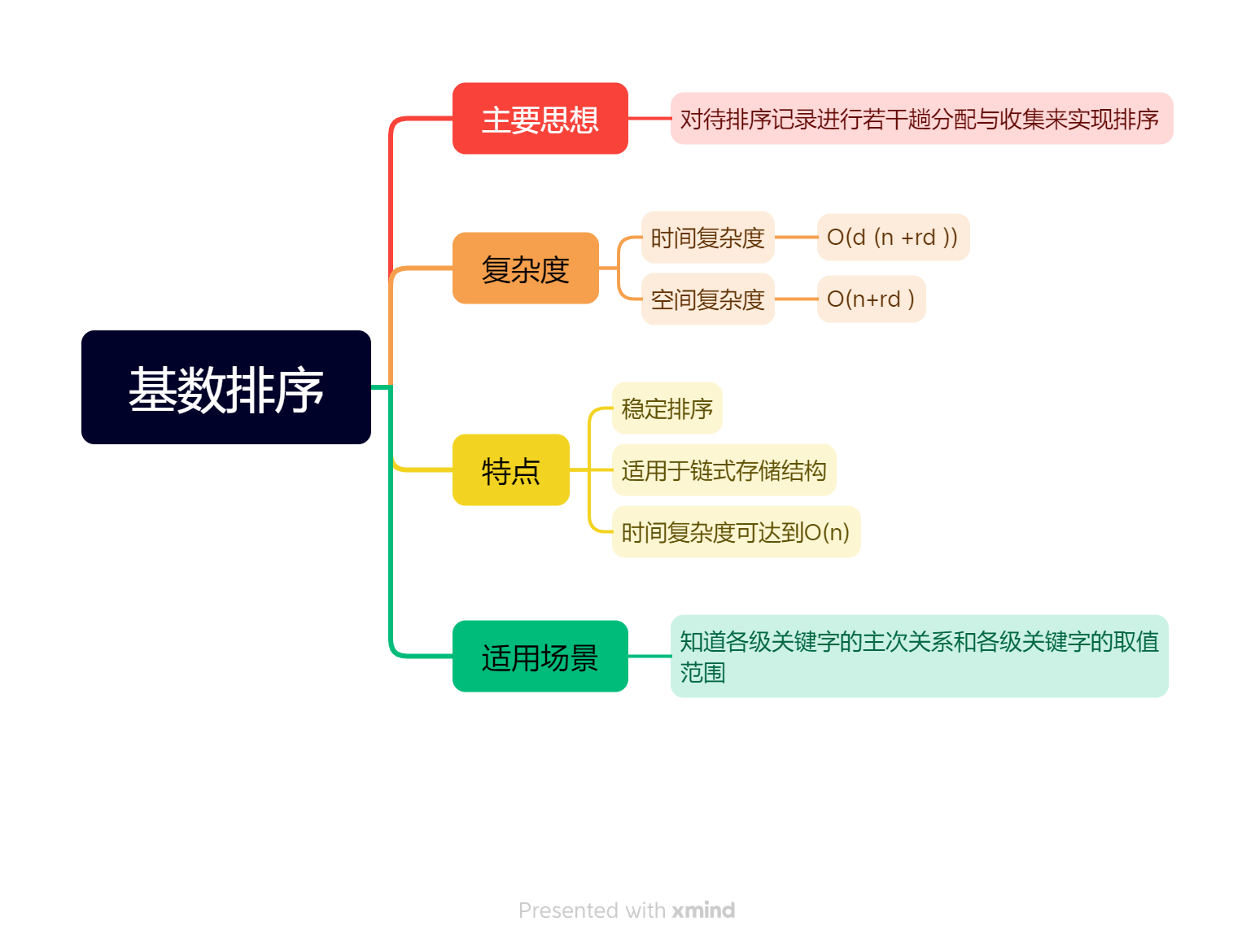
数据结构：分配排序

插入类、交换类、选择类和归并类排序方法，都是在比较关键字大小的基础上实现排序的，而分配类排序不需要比较关键字的大小。

分配排序，是指通过对待排序记录进行若干趟分配与收集实现排序，是一种借助多关键字排序思想对单关键字进行排序的方法。基数排序（Radix Sorting）是最典型的分配类排序。

一、多关键字排序思想

先看一个具体例子。已知一副扑克牌，52张牌面的次序关系为

♣2<♣3<...<♣A<
♦2<♦3<...<♦A<
♥2<♥3<...<♥A<
♠2<♠3<...<♠A

即，每张牌有两个关键字：花色（♣<♦<♥<♠）和面值（2<3<…<A），且花色的地位高于面值。在比较任意两张牌面的大小时，必须先比较花色，若花色相同，则再比较面值。由此，将扑克牌整理成上述次序关系时，有以下两种排序法。

最高位优先法：先按不同花色分成有次序的4堆，每堆牌均具有相同的花色，然后分别对每堆牌按面值大小整理有序。

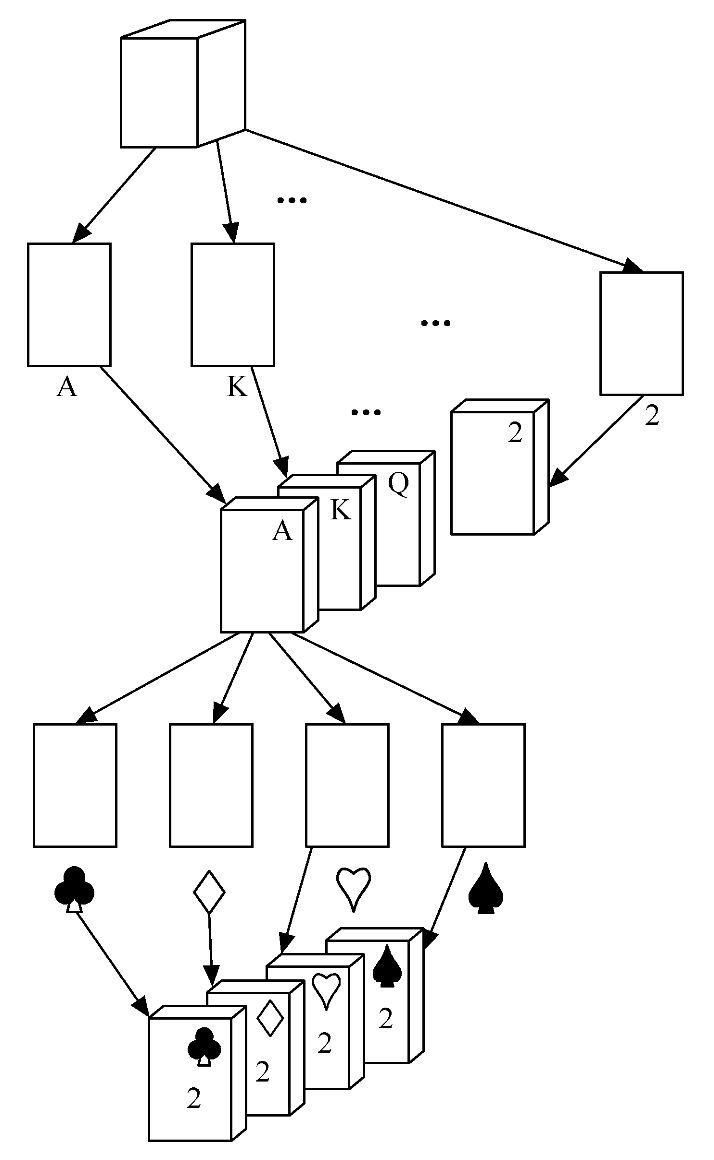
最低位优先法：先按不同面值分成13堆，然后将这13堆牌按照面值的次序收集到一起（将13堆牌自小至大叠在一起，3在2之上，4在3之上，…，最上面的是4张A）；再重新对这些牌按不同花色分成4堆，最后将这4堆牌按花色的次序再收集到一起（♣在最下面，♠在最上面）。此时，同样可以得到一副，满足上述次序关系的牌。该方法是一种分配与收集交替进行的方法，其过程如下图所示。

二、链式基数排序

2.1、算法思想

基数排序的思想类似于上述最低位优先法的洗牌过程，是借助分配和收集操作，对单逻辑关键字进行排序的一种内部排序方法。

有的逻辑关键字可以看成是由若干个关键字复合而成的。例如，若关键字是数值，且其值都在 $0\le K \le 999$ 范围内，则可把每位上的十进制数字看成一个关键字，即可认为K由3个关键字 $（K^0,K^1,K^2）$ 组成，其中 $k^0$ 是百位数， $k^1$ 是十位数， $k^2$ 是个位数；若关键字K是由5个字母组成的单词，则可看成是由5个关键字 $（K^0,K^1,K^2,K^3,K^4）$ 组成，其中 $k^{j-1}$ 是（自左至右的）第j个字母。这样分解而得的每个关键字 $k^j$ 都在相同的范围内（对数字来说，是 $0 \le k^j \le 9$ ；对于字母来说，是 $'A' \le k^j \le 'Z'$ ），故可以按照分配和收集的方法进行排序。

假设记录的逻辑关键字由d个关键字组成，每个关键字可能取rd个值。只要从最低数位关键字起，按关键字的不同值将序列中记录分配到rd个队列中后再收集之，如此重复d次完成排序。按这种方法实现排序称之为基数排序，其中“基”指的是rd的取值范围，在上述两种关键字的情况下，rd的取值范围分别为10和26。

2.1.1、示例

接下来，来看一个具体例子。

假设待排序记录的关键字都是数值，且值都在 $0\le K \le 999$ 范围内。首先，以链表存储n个待排序记录，链表头指针指向第一个记录，如图下所示。然后，通过三趟分配和收集操作来完成排序。

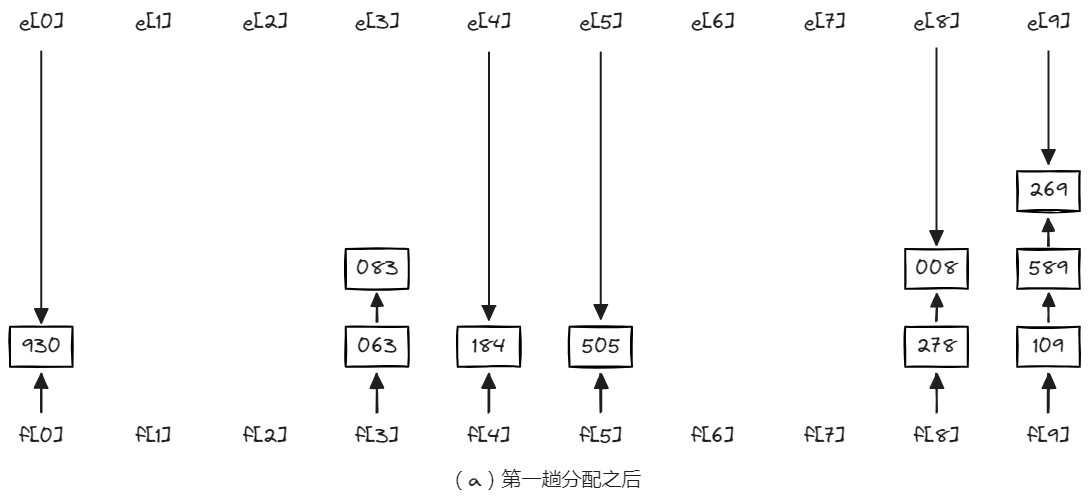
第一趟分配对最低数位关键字（个位数）进行，改变记录的指针值，将链表中的记录分配到10个链表中，每个链表中的记录关键字的个位数相等，如下图（a）所示，其中f[i]和e[i]分别为第i个链表的头指针和尾指针；第一趟收集是改变所有非空链表的表尾记录的指针域，令其指向下一个非空链表的表头记录，重新将10个链表中的记录链成一个链表，如下图（b）所示。

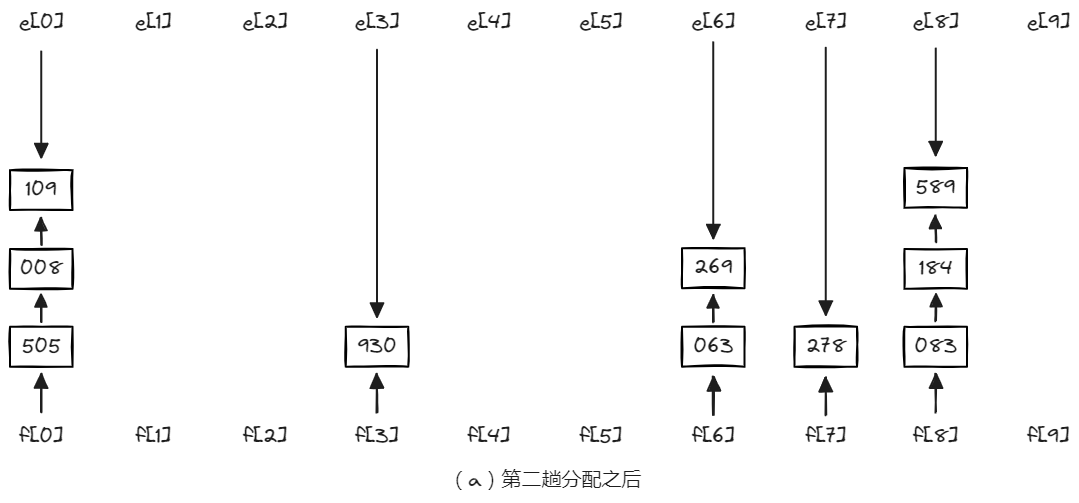
第二趟分配和第二趟收集是对十位数进行的，其过程和个位数相同。分配和收集结果分别如下图（a）和下图（b）所示。

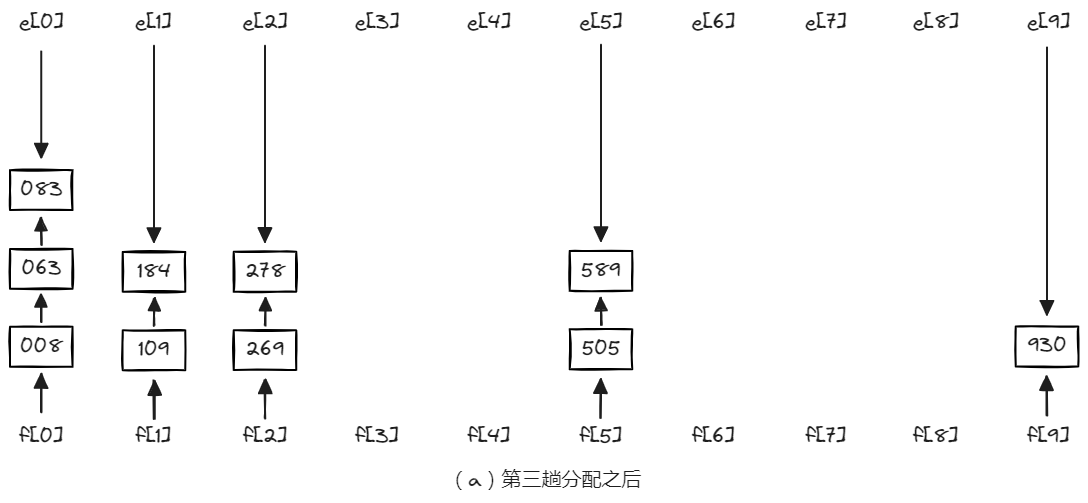
第三趟分配和第三趟收集是对百位数进行的，过程同上。分配和收集结果分别如下图（a）和下图（b）所示。至此排序完毕。

2.1.2、存储结构

基数排序在具体实现时，一般采用链式存储结构。这里，算法实现时采用静态链表（即用数组描述的链表），以便于更有效地存储和重排记录。相关数据类型的定义如下：

// 记录的逻辑关键字最多由多少个关键字组成（这里假设最多由8个关键字组成）
#define MAXNUM_KEY 8

// 关键字基数的取值范围（这里假设是十进制整数）
#define RADIX 10

// 静态链表的空间大小
#define MAX_SPACE 10000

// 静态链表的结点类型
typedef struct
{
  // 关键字
  KeyType keys[MAXNUM_KEY];
  // 其他数据项
  InfoType otheritems;
  int next;
}SLCell;

// 静态链表类型
typedef struct
{
  // 静态链表的可利用空间，r[0]为头结点
  SLCell r[MAX_SPACE];
  // 静态链表的当前长度
  int recnum;
  // 记录的当前关键字个数
  int keynum;
}SLList;

// 数组类型
typedef int ArrType[RADIX]

2.2、算法描述

// 静态链表L的r域中的记录已按（keys[0], keys[1],..., keys[i-1]）有序
// 按第i个关键字keys[i]建立RADIX个子表，keys[i]相同的记录存放在同一个子表中
// f[0..RADIX-1]和e[0..RADIX-1]分别指向各子表中第一个和最后一个记录
void Distribute(SLCell &r, int i, ArrType &f, ArrType &e)
{
  // 初始化各子表为空表
  for(j=0; j<RADIX; ++j) f[j]=0;

  for(p=r[0].next; p; p=r[p].next)
  {
    // ord函数根据记录的第i个关键字，将记录映射到某个子表（即求记录在子表中的位置）
    j=ord(r[p].keys[i]);

    // 将p所指的结点插入到第j个子表中
    if(!f[j]) f[j]=p;
    else r[e[j]].next=p;
    e[j]=p;
  }
}

// 按第i个关键字keys[i]自小到大地将f[0..RADIX-1]所指各子表依次链接成一个链表
// e[0..RADIX-1]为各子表的尾指针
void Collect(SLCell &r, int i, ArrType f, ArrType e)
{
  // 找第一个非空子表，succ函数是求后继函数
  for(j=0; !f[j]; j=succ(j));
    
  // 静态链表的头节点r[0]指向第一个非空子表中第一个结点
  r[0].next=f[j];
  // t指向最后一个非空子表中的最后一个结点
  t=e[j];
 
  while(j<RADIX)
  {
    // 找下一个非空子表
    for(j=succ(j); j<RADIX-1&&!f[j]; j=succ(j));
    // 链接两个非空子表
    if(f[j]) { r[t].next=f[j]; t=e[j]; }
  }
  // 将最后一个结点的指针域置空
  r[t].next=0;
}

// 对L（采用静态链表表示的顺序表）做基数排序，使得L成为按关键字自小到大的有序静态链表
void RadixSort(SLList &L)
{
  // 将L改造为静态链表，r[0]为头结点
  for(i=0;i<L.recnum;++i) L.r[i].next=i+1;
  L.r[L.recnum].next=0;

  // 按最低位优先法，依次对各个关键字进行分配和收集
  for(i=0;i<L.keynum;++i) {
    // 第i趟分配
    Distribute(L.r, i, f, e);
    // 第i趟收集
    Collect(L.r, i, f, e);
  }
}